机器学习实战-逻辑回归

逻辑回归

数据集 | 社交网络

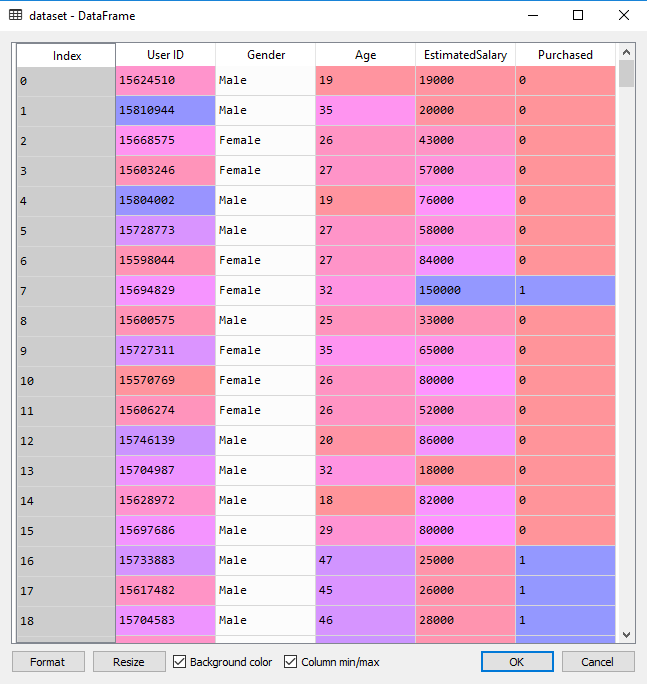
该数据集包含了社交网络中用户的信息。这些信息涉及用户 ID,性别,年龄以及预估薪资。一家汽车公司刚刚推出了他们新型的豪华 SUV，我们尝试预测哪些用户会购买这种全新 SUV 。并且在最后一列用来表示用户是否购买。我们将建立一种模型来预测用户是否购买这种 SUV，该模型基于两个变量，分别是年龄和预计薪资。因此我们的特征矩阵将是这两列。我们尝试寻找用户年龄与预估薪资之间的某种相关性，以及他是否购买 SUV 的决定。

步骤1 | 数据预处理

导入库

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

导入数据集

这里获取数据集

dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
Y = dataset.iloc[:, 4].values

将数据集分成训练集和测试集

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.25, random_state=0)

特征缩放

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

步骤2 | 逻辑回归模型

该项工作的库将会是一个线性模型库，之所以被称为线性是因为逻辑回归是一个线性分类器，这意味着我们在二维空间中，我们两类用户（购买和不购买）将被一条直线分割。然后导入逻辑回归类。下一步我们将创建该类的对象，它将作为我们训练集的分类器。

将逻辑回归应用于训练集

from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression()
classifier.fit(X_train, y_train)

步骤3 | 预测与评估

预测测试集结果

y_pred = classifier.predict(X_test)

评估：生成混淆矩阵

我们预测了测试集。 现在我们将评估逻辑回归模型是否正确的学习和理解。因此这个混淆矩阵将包含我们模型的正确和错误的预测。

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)

打印混淆矩阵 cm

[[65  3]
 [ 8 24]]

可视化

from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np. meshgrid(np. arange(start=X_set[:, 0].min()-1, stop=X_set[:, 0].max()+1, step=0.01),
                   np. arange(start=X_set[:, 1].min()-1, stop=X_set[:, 1].max()+1, step=0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha=0.75, cmap=ListedColormap(('red', 'green')))
plt.xlim(X1.min(),X1.max())
plt.ylim(X2.min(),X2.max())
for i, j in enumerate(np. unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c=ListedColormap(('red', 'green'))(i), label=j)

plt. title(' LOGISTIC(Training set)')
plt. xlabel(' Age')
plt. ylabel(' Estimated Salary')
plt. legend()
plt. show()

X_set, y_set = X_test, y_test
X1, X2 = np. meshgrid(np. arange(start=X_set[:, 0].min()-1, stop=X_set[:, 0].max()+1, step=0.01),
                   np. arange(start=X_set[:, 1].min()-1, stop=X_set[:, 1].max()+1, step=0.01))

plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha=0.75, cmap=ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np. unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c=ListedColormap(('red', 'green'))(i), label=j)

plt. title(' LOGISTIC(Test set)')
plt. xlabel(' Age')
plt. ylabel(' Estimated Salary')
plt. legend()
plt. show()

可视化结果如下图：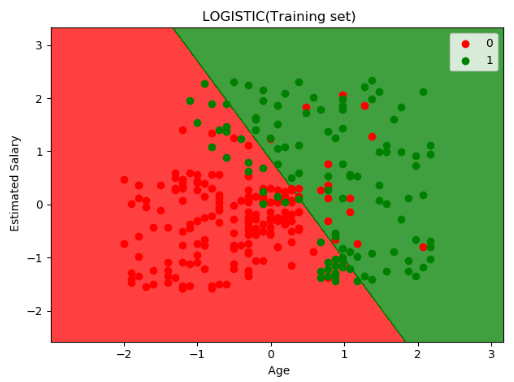

softmax 回归

逻辑回归中的 softmax 机制

Logistic 回归模型可以直接推广到支持多类别分类任务，不必组合和训练多个二分类器，其称为Softmax 回归或多类别 Logistic 回归。

这个想法很简单：当给定一个实例 $\mathbf{x}$ 时，Softmax 回归模型首先计算 $k$ 类的分数 $s_k(\mathbf{x})$，然后将分数应用在Softmax函数（也称为归一化指数）上，估计出每类的概率。计算 $s_k(\mathbf{x})$ 的公式看起来很熟悉，因为它就像线性回归预测的公式一样。

$$s_k(\mathbf{x}) = \theta_k^T \cdot \mathbf{x} $$

注意，每个类都有自己独一无二的参数向量 $\theta_k$。所有这些向量通常作为行放在参数矩阵 $\Theta$ 中。

模型训练

当你使用 LogisticRregression 对模型进行训练时，Scikit Learn 默认使用的是一对多模型，但是你可以设置 multi_class 参数为 “multinomial” 来把它改变为 Softmax 回归。你还必须指定一个支持 Softmax 回归的求解器，例如 “lbfgs” 求解器（有关更多详细信息，请参阅 Scikit-Learn 的文档）。其默认使用 $\ell_2$ 正则化，你可以使用超参数 $C$ 控制它。

from sklearn.linear_model import LogisticRegression
softmax_reg = LogisticRegression(multi_class="multinomial", solver="lbfgs", C=10)
softmax_reg.fit(X, y)

参考链接

机器学习100天