机器学习实战-支持向量机 SVM

基本步骤

数据集

社交网络-Social_Network_Ads.csv

第 1 步：导入库

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

第 2 步：导入数据

dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values

第 3 步：拆分数据集为训练集合和测试集合

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)

第 4 步：特征量化

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.fit_transform(X_test)

第 5 步：适配 SVM 到训练集合

from sklearn.svm import SVC
classifier = SVC(kernel='linear', random_state=0)
classifier.fit(X_train, y_train)

第 6 步：预测测试集合结果

y_pred = classifier.predict(X_test)

第 7 步：创建混淆矩阵

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)

打印混淆矩阵结果：

[[63  5]
 [ 7 25]]

第 8 步：训练集合结果可视化

from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start=X_set[:, 0].min() - 1, stop=X_set[:, 0].max() + 1, step=0.01),
                     np.arange(start=X_set[:, 1].min() - 1, stop=X_set[:, 1].max() + 1, step=0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha=0.75, cmap=ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c=ListedColormap(('red', 'green'))(i), label=j)
plt.title('SVM (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()

运行结果如下图：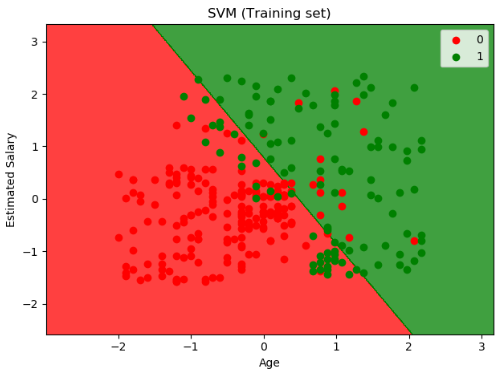

第 9 步：测试集合结果可视化

from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start=X_set[:, 0].min() - 1, stop=X_set[:, 0].max() + 1, step=0.01),
                     np.arange(start=X_set[:, 1].min() - 1, stop=X_set[:, 1].max() + 1, step=0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha=0.75, cmap=ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c=ListedColormap(('red', 'green'))(i), label=j)
plt.title('SVM (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()

运行结果如下图：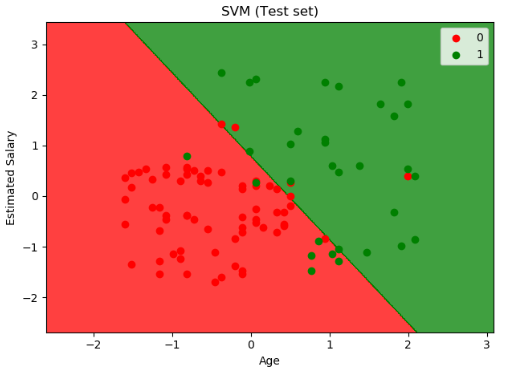

SVM 分类

线性支持向量机分类

以下的 Scikit-Learn 代码使用流水线进行缩放特征，并训练一个线性 SVM 模型（使用 LinearSVC 类，超参数 C=1， hinge 损失函数），其中 X 为训练集特征， y 为训练集标签。

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
svm_clf = Pipeline((
        ("scaler", StandardScaler()),
        ("linear_svc", LinearSVC(C=1, loss="hinge", dual=False)),
    ))
svm_clf.fit(X, y)

提示

LinearSVC 要使偏置项规范化，首先你应该集中训练集减去它的平均数。如果你使用了 StandardScaler ，那么它会自动处理。此外，确保你设置 loss 参数为 hinge，因为它不是默认值。最后，为了得到更好的效果，你需要将 dual 参数设置为 False ，除非特征数比样本量多。

不同于 Logistic 回归分类器，SVM 分类器不会输出每个类别的概率。

作为一种选择，你可以在 SVC 类，使用 SVC(kernel="linear", C=1) ，但是它比较慢，尤其在较大的训练集上，所以一般不被推荐。

另一个选择是使用 SGDClassifier 类，即 SGDClassifier(loss="hinge", alpha=1/(m*C)) 。它应用了随机梯度下降来训练一个线性 分类器。尽管它不会和 LinearSVC 一样快速收敛，但是对于处理那些不适合放在内存的大数据集是非常有用的，或者处理在线分类任务同样有用。

非线性支持向量机分类

一般非线性

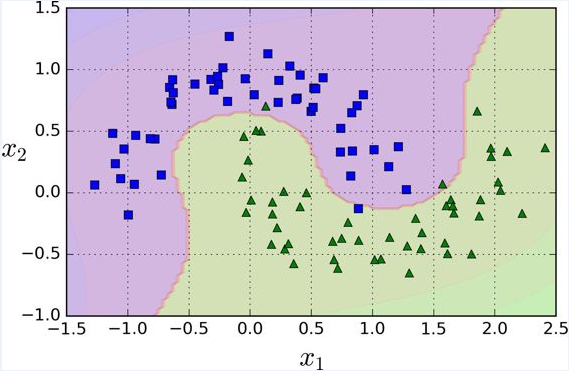
尽管线性 SVM 分类器在许多案例上表现得出乎意料的好，但是很多数据集并不是线性可分的。一种处理非线性数据集方法是增加更多的特征，例如多项式特征；在某些情况下可以变成线性可分的数据。在下图的左图中，它只有一个特征 x1 的简单的数据集，正如你看到的，该数据集不是线性可分的。但是如果你增加了第二个特征 x2=(x1)^2 ，产生的 2D 数据集就能很好的线性可分。

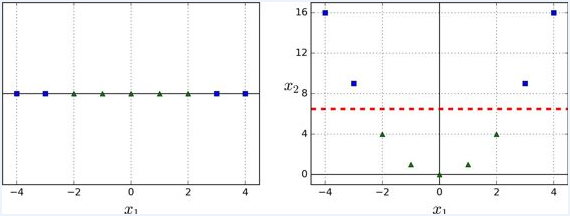
为了实施这个想法，通过 Scikit-Learn，你可以创建一个流水线（Pipeline）去包含多项式特征（PolynomialFeatures）变换，然后一个 StandardScaler 和 LinearSVC 。让我们在卫星数据集（moons datasets）测试一下效果。

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

polynomial_svm_clf = Pipeline((
        ("poly_features", PolynomialFeatures(degree=3)),
        ("scaler", StandardScaler()),
        ("svm_clf", LinearSVC(C=10, loss="hinge"))
    ))

polynomial_svm_clf.fit(X, y)

多项式核

添加多项式特征很容易实现，不仅仅在 SVM，在各种机器学习算法都有不错的表现，但是低次数的多项式不能处理非常复杂的数据集，而高次数的多项式却产生了大量的特征，会使模型变得慢。幸运的是，当你使用 SVM 时，你可以运用一个被称为“核技巧”（kernel trick）的神奇数学技巧。它可以取得就像你添加了许多多项式，甚至有高次数的多项式，一样好的结果。所以不会大量特征导致的组合爆炸，因为你并没有增加任何特征。这个技巧可以用 SVC 类来实现。让我们在卫星数据集测试一下效果。

from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline((
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
    ))
poly_kernel_svm_clf.fit(X, y)

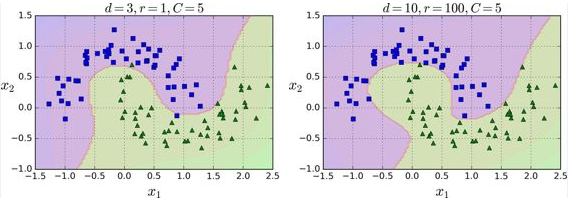
这段代码用3阶的多项式核训练了一个 SVM 分类器，如下图的左图。右图是使用了 10 阶的多项式核 SVM 分类器。很明显，如果你的模型过拟合，你可以减小多项式核的阶数。相反的，如果是欠拟合，你可以尝试增大它。超参数 coef0 控制了高阶多项式与低阶多项式对模型的影响。

高斯 RBF 核

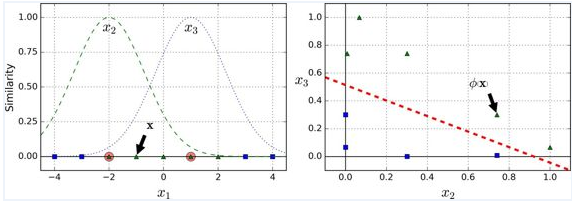
另一种解决非线性问题的方法是使用相似函数（similarity funtion）计算每个样本与特定地标（landmark）的相似度。例如，让我们来看看前面讨论过的一维数据集，并在 x1=-2 和 x1=1 之间增加两个地标（上图 左图）。接下来，我们定义一个相似函数，即高斯径向基函数（Gaussian Radial Basis Function，RBF），设置 γ = 0.3（公式如下）

$\phi_{\gamma}(x, \ell) = exp(-\gamma |x - \ell |^2)$

它是个从 0 到 1 的钟型函数，值为 0 的离地标很远，值为 1 的在地标上。现在我们准备计算新特征。例如，我们看一下样本 x1=-1 ：它距离第一个地标距离是 1，距离第二个地标是 2。因此它的新特征为 x2=exp(-0.3 × (1^2))≈0.74 和 x3=exp(-0.3 × (2^2))≈0.30 。上图右边的图显示了特征转换后的数据集（删除了原始特征），正如你看到的，它现在是线性可分了。

你可能想知道如何选择地标。最简单的方法是在数据集中的每一个样本的位置创建地标。这将产生更多的维度从而增加了转换后数据集是线性可分的可能性。但缺点是，m 个样本，n 个特征的训练集被转换成了 m 个实例，m 个特征的训练集（假设你删除了原始特征）。这样一来，如果你的训练集非常大，你最终会得到同样大的特征。

就像多项式特征法一样，相似特征法对各种机器学习算法同样也有不错的表现。但是在所有额外特征上的计算成本可能很高，特别是在大规模的训练集上。然而，“核” 技巧再一次显现了它在 SVM 上的神奇之处：高斯核让你可以获得同样好的结果成为可能，就像你在相似特征法添加了许多相似特征一样，但事实上，你并不需要在RBF添加它们。我们使用 SVC 类的高斯 RBF 核来检验一下。

rbf_kernel_svm_clf = Pipeline((
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
    ))
rbf_kernel_svm_clf.fit(X, y)

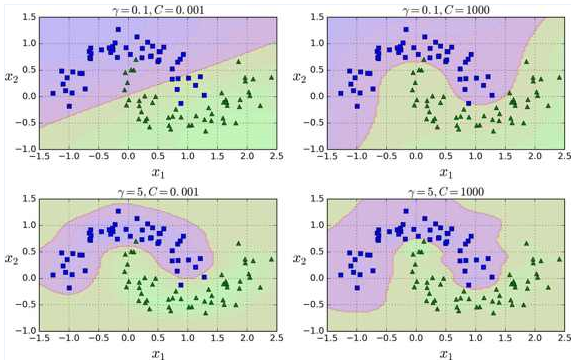
这个模型在下图的左下角表示。其他的图显示了用不同的超参数 gamma (γ) 和 C 训练的模型。增大 γ 使钟型曲线更窄（下图左图），导致每个样本的影响范围变得更小：即判定边界最终变得更不规则，在单个样本周围环绕。相反的，较小的 γ 值使钟型曲线更宽，样本有更大的影响范围，判定边界最终则更加平滑。所以 γ 是可调整的超参数：如果你的模型过拟合，你应该减小 γ 值，若欠拟合，则增大 γ （与超参数 C 相似）。

核函数如何选择？★

这么多可供选择的核函数，你如何决定使用哪一个？一般来说，你应该先尝试线性核函数（记住 LinearSVC 比 SVC(kernel="linear") 要快得多），尤其是当训练集很大或者有大量的特征的情况下。如果训练集不太大，你也可以尝试高斯径向基核（Gaussian RBF Kernel），它在大多数情况下都很有效。如果你有空闲的时间和计算能力，你还可以使用交叉验证和网格搜索来试验其他的核函数，特别是有专门用于你的训练集数据结构的核函数。

SVM 回归

线性回归任务

正如我们之前提到的，SVM 算法应用广泛：不仅仅支持线性和非线性的分类任务，还支持线性和非线性的回归任务。技巧在于逆转我们的目标：限制间隔违规的情况下，不是试图在两个类别之间找到尽可能大的“街道”（即间隔）。SVM 回归任务是限制间隔违规情况下，尽量放置更多的样本在“街道”上。“街道”的宽度由超参数 ϵ 控制。下图显示了在一些随机生成的线性数据上，两个线性 SVM 回归模型的训练情况。一个有较大的间隔（ ϵ=1.5 ），另一个间隔较小（ ϵ=0.5 ）。

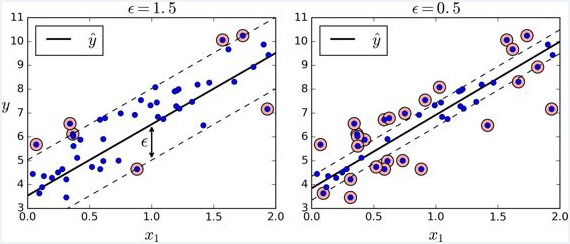
添加更多的数据样本在间隔之内并不会影响模型的预测，因此，这个模型认为是不敏感的（ϵ-insensitive）。

你可以使用 Scikit-Learn 的 LinearSVR 类去实现线性 SVM 回归。下面的代码产生的模型在上图左图（训练数据需要被中心化和标准化）

from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5)
svm_reg.fit(X, y)

非线性回归任务

处理非线性回归任务，你可以使用核化的 SVM 模型。比如，下图显示了在随机二次方的训练集，使用二次方多项式核函数的 SVM 回归。左图是较小的正则化（即更大的 C 值），右图则是更大的正则化（即小的 C 值）

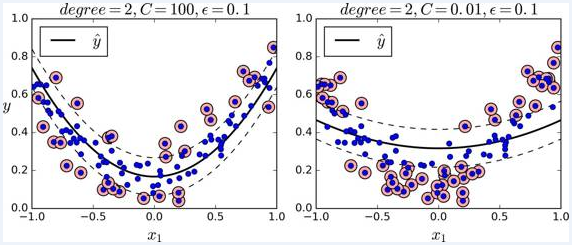
下面的代码的模型在上图中，其使用了 Scikit-Learn 的 SVR 类（支持核技巧）。在回归任务上， SVR 类和 SVC 类是一样的，并且 LinearSVR 是和 LinearSVC 等价。 LinearSVR 类和训练集的大小成线性（就像 LinearSVC 类），当训练集变大， SVR 会变的很慢（就像 SVC 类）

from sklearn.svm import SVR
svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1)
svm_poly_reg.fit(X, y)

SVM 异常值检测

详情见 Scikit-Learn 文档，以后补充。

调参 ★

SVM 分类算法库参数小结

这里我们对SVM分类算法库的重要参数做一个详细的解释，重点讲述调参的一些注意点。

参数	LinearSVC	SVC	NuSVC
惩罚系数C	即为我们第二节中 SVM 分类模型原型形式和对偶形式中的惩罚系数 C，默认为 1，一般需要通过交叉验证来选择一个合适的 C。一般来说，如果噪音点较多时，C 需要小一些。		NuSVC 没有这个参数, 它通过另一个参数 nu 来控制训练集训练的错误率，等价于选择了一个 C，让训练集训练后满足一个确定的错误率
nu	LinearSVC 和 SVC 没有这个参数，LinearSVC 和 SVC 使用惩罚系数 C 来控制惩罚力度。		nu 代表训练集训练的错误率的上限，或者说支持向量的百分比下限，取值范围为(0,1],默认是0.5.它和惩罚系数 C 类似，都可以控制惩罚的力度。
核函数 kernel	LinearSVC 没有这个参数，LinearSVC 限制了只能使用线性核函数	核函数有四种内置选择，第三节已经讲到：'linear' 即线性核函数, 'poly' 即多项式核函数, 'rbf' 即高斯核函数, 'sigmoid' 即 sigmoid 核函数。如果选择了这些核函数， 对应的核函数参数在后面有单独的参数需要调。默认是高斯核 'rbf'。 还有一种选择为 "precomputed"，即我们预先计算出所有的训练集和测试集的样本对应的 Gram 矩阵，这样 K(x,z) 直接在对应的 Gram 矩阵中找对应的位置的值。
正则化参数 penalty	仅仅对线性拟合有意义，可以选择 'l1' 即 L1 正则化 或者 'l2' 即 L2 正则化。默认是 L2 正则化，如果我们需要产生稀疏话的系数的时候，可以选 L1 正则化,这和线性回归里面的 Lasso 回归类似。	SVC 和 NuSVC 没有这个参数
是否用对偶形式优化 dual	这是一个布尔变量，控制是否使用对偶形式来优化算法，默认是 True，即采用上面第二节的分类算法对偶形式来优化算法。如果我们的样本量比特征数多，此时采用对偶形式计算量较大，推荐 dual 设置为 False，即采用原始形式优化	SVC 和 NuSVC 没有这个参数
核函数参数 degree	LinearSVC 没有这个参数	如果我们在 kernel 参数使用了多项式核函数 'poly'，那么我们就需要对这个参数进行调参。这个参数对应 K(x,z)=（γx∙z+r)^d 中的 d。默认是3。一般需要通过交叉验证选择一组合适的 γ,r,d
核函数参数 gamma	LinearSVC 没有这个参数	如果我们在 kernel 参数使用了多项式核函数 'poly'，高斯核函数 ‘rbf’, 或者 sigmoid 核函数，那么我们就需要对这个参数进行调参。γ 默认为 'auto',即 1/特征维度。
核函数参数 coef0	LinearSVC 没有这个参数	如果我们在 kernel 参数使用了多项式核函数 'poly'，或者 'sigmoid' 核函数，那么我们就需要对这个参数进行调参。coef0默认为 0
样本权重 class_weight	指定样本各类别的的权重，主要是为了防止训练集某些类别的样本过多，导致训练的决策过于偏向这些类别。这里可以自己指定各个样本的权重，或者用 “balanced”，如果使用 “balanced”，则算法会自己计算权重，样本量少的类别所对应的样本权重会高。当然，如果你的样本类别分布没有明显的偏倚，则可以不管这个参数，选择默认的 "None"
分类决策 decision_function_shape	LinearSVC 没有这个参数，使用 multi_class 参数替代。	可以选择'ovo'或者'ovr'.目前0.18版本默认是'ovo'.0.19版本将是'ovr' OvR(one ve rest)的思想很简单，无论你是多少元分类，我们都可以看做二元分类。具体做法是，对于第K类的分类决策，我们把所有第K类的样本作为正例，除了第K类样本以外的所有样本都作为负例，然后在上面做二元分类，得到第K类的分类模型。其他类的分类模型获得以此类推。 OvO(one-vs-one)则是每次每次在所有的T类样本里面选择两类样本出来，不妨记为T1类和T2类，把所有的输出为T1和T2的样本放在一起，把T1作为正例，T2作为负例，进行二元分类，得到模型参数。我们一共需要T(T-1)/2次分类。 从上面的描述可以看出OvR相对简单，但分类效果相对略差（这里指大多数样本分布情况，某些样本分布下OvR可能更好）。而OvO分类相对精确，但是分类速度没有OvR快。一般建议使用OvO以达到较好的分类效果。
分类决策 multi_class	可以选择 'ovr' 或者 'crammer_singer' 'ovr'和 SVC 和 nuSVC 中的 decision_function_shape 对应的'ovr'类似。 'crammer_singer'是一种改良版的'ovr'，说是改良，但是没有比'ovr'好，一般在应用中都不建议使用。	SVC 和 nuSVC 没有这个参数，使用 decision_function_shape 参数替代。
缓存大小 cache_size	LinearSVC 计算量不大，因此不需要这个参数	在大样本的时候，缓存大小会影响训练速度，因此如果机器内存大，推荐用 500MB 甚至 1000MB。默认是 200，即 200MB.

SVM 回归算法库参数小结

SVM 回归算法库的重要参数巨大部分和分类算法库类似，因此这里重点讲述和分类算法库不同的部分，对于相同的部分可以参考上一节对应参数。

参数	LinearSVR	SVR	NuSVR
惩罚系数 C	即为我们第二节中 SVM 分类模型原型形式和对偶形式中的惩罚系数 C，默认为 1，一般需要通过交叉验证来选择一个合适的 C。一般来说，如果噪音点较多时，C 需要小一些。大家可能注意到在分类模型里面，nuSVC 使用了 nu 这个等价的参数控制错误率，就没有使用 C，为什么我们 nuSVR 仍然有这个参数呢，不是重复了吗？这里的原因在回归模型里面，我们除了惩罚系数 C 还有还有一个距离误差 ϵ 来控制损失度量，因此仅仅一个 nu 不能等同于 C.也就是说回归错误率是惩罚系数 C 和距离误差 ϵ 共同作用的结果。后面我们可以看到 nuSVR中nu 的作用。
nu	LinearSVR 和 SVR 没有这个参数，用 ϵ 控制错误率		nu 代表训练集训练的错误率的上限，或者说支持向量的百分比下限，取值范围为 (0,1] ，默认是 0.5 。通过选择不同的错误率可以得到不同的距离误差ϵ 。也就是说这里的 nu 的使用和 LinearSVR 和 SVR 的 ϵ 参数等价。
距离误差 epsilon	即我们第二节回归模型中的 ϵ，训练集中的样本需满足 −ϵ−ξ∨i≤yi−w∙ϕ(xi)−b≤ϵ+ξ∧i		nuSVR 没有这个参数，用 nu 控制错误率
是否用对偶形式优化 dual	和SVC类似，可参考上一节的 dual 描述	SVR 和 NuSVR 没有这个参数
正则化参数 penalty	和SVC类似，可参考上一节的 penalty 描述	SVR 和 NuSVR 没有这个参数
核函数 kernel	LinearSVR 没有这个参数	和 SVC, nuSVC 类似，可参考上一节的 kernel 描述
核函数参数 degree, gamma 和 coef0	LinearSVR 没有这个参数	和 SVC, nuSVC 类似，可参考上一节的 kernel 参数描述
损失函数度量 loss	可以选择为 'epsilon_insensitive' 和 'squared_epsilon_insensitive'	SVR 和 NuSVR 没有这个参数
缓存大小 cache_size	LinearSVC 计算量不大，因此不需要这个参数	在大样本的时候，缓存大小会影响训练速度，因此如果机器内存大，和 SVC，nuSVC 一样，推荐用 500MB 甚至 1000MB 。默认是 200，即 200MB 。

SVM 算法调参要点

上面已经对 scikit-learn 中类库的参数做了总结，这里对其他的调参要点做一个小结。

1. 一般推荐在做训练之前对数据进行归一化，当然测试集中的数据也需要归一化。。
2. 在特征数非常多的情况下，或者样本数远小于特征数的时候，使用线性核，效果已经很好，并且只需要选择惩罚系数 C 即可。
3. 在选择核函数时，如果线性拟合不好，一般推荐使用默认的高斯核 ‘rbf’。这时我们主要需要对惩罚系数 C 和核函数参数 γ 进行艰苦的调参，通过多轮的交叉验证选择合适的惩罚系数 C 和核函数参数γ。
4. 理论上高斯核不会比线性核差，但是这个理论却建立在要花费更多的时间来调参上。所以实际上能用线性核解决问题我们尽量使用线性核。

调参实例 ★

以高斯核函数 NuSVC 进行调参示例演练，这里我选取 《kaggle 泰坦尼克：从灾难中学习算法》中经过数据处理的数据集。假设 train_X 为训练特征， train_y 为训练标签，高斯核函数支持向量分类器主要需要调整的参数有两个 nu 和 gamma. 基于分类任务的评价指标指标有很多，我们这里选取 scoring='accuracy' ，有兴趣的同学也可以尝试其他的评价指标，比如 'f1' 'roc_auc' 等。

导入相关的库

from sklearn.svm import NuSVC
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV

搜索参数 nu 的最优取值范围

nu_list = np.linspace(0.1, 0.7, 7)
accuracy_scroes = []
for nu in nu_list:
    nusvc = NuSVC(nu=nu)
    scores_accuracy = cross_val_score(nusvc, train_X, train_y, scoring='accuracy', cv=5)
    accuracy_scroes.append(scores_accuracy.mean())

打印曲线图

plt.plot(nu_list, accuracy_scroes)
plt.title("nu for accuracy_scroes")

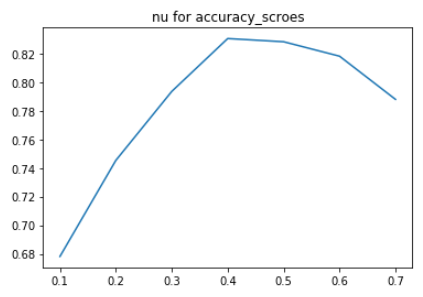
如上图可知，最佳 nu 值出现在 0.4 左右，所以网格搜索我们设定 nu 的取值范围在 [0.3, 0.6] 之间。

搜索参数 gamma 的最优取值范围

gamma_list = np.linspace(0.01, 1, 91)
accuracy_scroes = []
for gamma in gamma_list:
    nusvc = NuSVC(gamma=gamma, nu=0.4)
    scores_accuracy = cross_val_score(nusvc, train_X, train_y, scoring='accuracy', cv=5)
    accuracy_scroes1.append(scores_accuracy.mean())

打印曲线图

plt.plot(gamma_list, accuracy_scroes)
plt.title("gamma for accuracy_scroes")

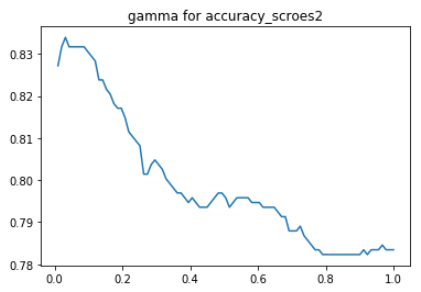
如上图可知，最佳 gamma 值出现在 0.02 左右，所以网格搜索我们设定 gamma 的取值范围在 (0, 0.2] 之间。

网格搜索

param_grid = {'nu': np.linspace(0.3, 0.6, 31), 'gamma': np.linspace(0.01, 0.2, 191)}
gsearch = GridSearchCV(NuSVC(), param_grid=param_grid, scoring='accuracy', cv=5)
gsearch.fit(train_X, train_y)
print(gsearch.best_params_)
print(gsearch.best_score_)

输出结果为：

{'gamma': 0.019000000000000003, 'nu': 0.39}
0.8338945005611672

所以 gamma=0.019 nu=0.39 即为最优参数.

参考链接

机器学习100天
Scikit-Learn