机器学习实战-K近邻法 K-NN

数据集 | 社交网络

第 1 步：导入相关库

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

第 2 步：导入数据集

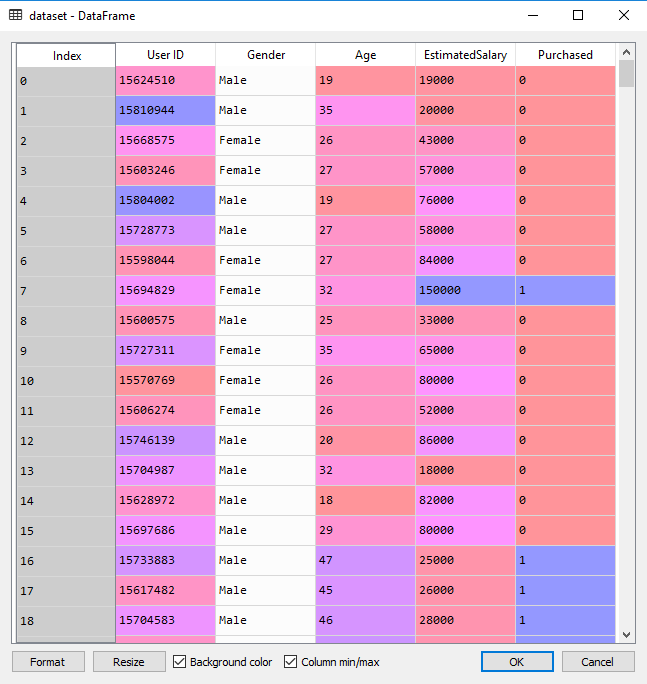
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values

为了方便理解，这里我们只取 Age 年龄和 EstimatedSalary 估计工资作为特征。

第 3 步：将数据划分成训练集和测试集

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)

第 4 步：特征缩放

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

这里有必要说明一下 fit_transform 和 transform 的区别。前者是 fit 和 transform 的结合， fit_transform(X_train) 意思是找出 X_train 的 $\mu$ 和 $\sigma$，并应用在 X_train 上。
这时对于 X_test，我们就可以直接使用 transform 方法。因为此时 StandardScaler 已经保存了 X_train 的 $\mu$ 和 $\sigma$ 。

为什么可以用训练集的 $\mu$ 和 $\sigma$ 来 transform 测试集的数据 X_train? 机器学习中有很多假设，这里假设了训练集的样本采样足够充分。

第 5 步：使用K-NN对训练集数据进行训练

从 sklearn 的 neighbors 类中导入 KNeighborsClassifier 学习器。

from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifier(n_neighbors=5, metric='minkowski', p=2)
classifier.fit(X_train, y_train)

设置好相关的参数 n_neighbors = 5 (K值的选择，默认选择5)、metric = 'minkowski' (距离度量的选择，这里选择的是闵氏距离(默认参数))、 p = 2 (距离度量 metric 的附属参数，只用于闵氏距离和带权重闵氏距离中 p 值的选择，p=1 为曼哈顿距离， p=2 为欧式距离。默认为2)

第 6 步：对测试集进行预测

y_pred = classifier.predict(X_test)

第 7 步：生成混淆矩阵

混淆矩阵可以对一个分类器性能进行分析，由此可以计算出许多指标，例如：ROC 曲线、正确率等。

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)

打印混淆矩阵，cm 结果为：

[[64  4]
 [ 3 29]]

预测集中的 0 总共有 68 个，1 总共有 32 个。 在这个混淆矩阵中，实际有 68 个 0，但 K-NN 预测出有 67(64+3) 个 0，其中有 3 个实际上是 1 。 同时 K-NN 预测出有 33(4+29) 个 1，其中 4 个实际上是 0 。

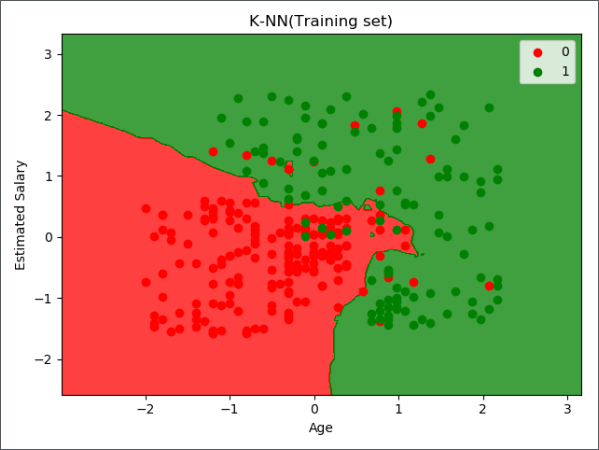
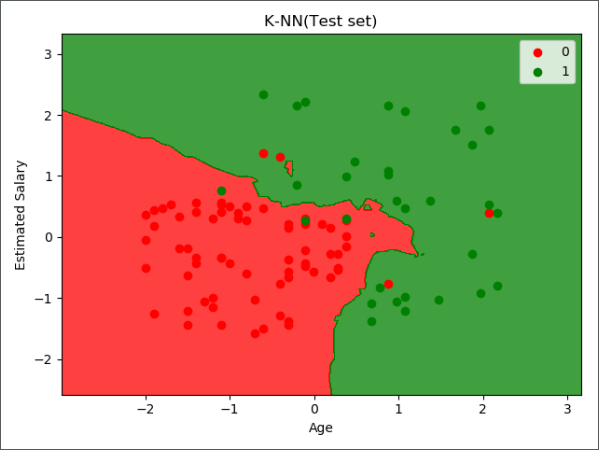
第 8 步：可视化

可视化相关代码详见另一篇文章《机器学习实战-逻辑回归》

参考链接

机器学习100天