数据集
| Country | Age | Salary | Purchased |
|---|---|---|---|
| France | 44 | 72000 | No |
| Spain | 27 | 48000 | Yes |
| Germany | 30 | 54000 | No |
| Spain | 38 | 61000 | No |
| Germany | 40 | Yes | |
| France | 35 | 58000 | Yes |
| Spain | 52000 | No | |
| France | 48 | 79000 | Yes |
| Germany | 50 | 83000 | No |
| France | 37 | 67000 | Yes |
第1步:导入库
这两个是我们每次都需要导入的库。NumPy 包含数学计算函数。Pandas 用于导入和管理数据集。1
2import numpy as np
import pandas as pd
第2步:导入数据集
数据集通常是 .csv 格式。 csv 文件以文本形式保存表格数据。文件的每一行是一条数据记录。我们使用 Pandas 的 read_csv 方法读取本地 csv 文件为一个数据帧。然后,从数据帧中制作自变量和因变量的矩阵和向量。1
2
3dataset = pd.read_csv('Data.csv') # 读取csv文件
X = dataset.iloc[ : , :-1].values # 不包括最后一列的所有列(.iloc[行,列])
Y = dataset.iloc[ : , 3].values # 取最后一列(: 全部行 or 列;[a] 第a行 or 列 )
打印 X 和 Y 运行结果如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14Step 2: Importing dataset
X
[['France' 44.0 72000.0]
['Spain' 27.0 48000.0]
['Germany' 30.0 54000.0]
['Spain' 38.0 61000.0]
['Germany' 40.0 nan]
['France' 35.0 58000.0]
['Spain' nan 52000.0]
['France' 48.0 79000.0]
['Germany' 50.0 83000.0]
['France' 37.0 67000.0]]
Y
['No' 'Yes' 'No' 'No' 'Yes' 'Yes' 'No' 'Yes' 'No' 'Yes']
第3步:处理丢失数据
我们得到的数据很少是完整的。数据可能因为各种原因丢失,为了不降低机器学习模型的性能,需要处理数据。我们可以用整列的平均值或中间值替换丢失的数据。我们用 sklearn.preprocessing 库中的 Imputer 类完成这项任务。1
2
3
4
5from sklearn.preprocessing import Imputer
# axis=0表示按列进行
imputer = Imputer(missing_values = "NaN", strategy = "mean", axis = 0)
imputer = imputer.fit(X[ : , 1:3])
X[ : , 1:3] = imputer.transform(X[ : , 1:3])
打印 imputer 和 X 运行结果如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14Step 3: Handling the missing data
imputer
Imputer(axis=0, copy=True, missing_values='NaN', strategy='mean', verbose=0)
X
[['France' 44.0 72000.0]
['Spain' 27.0 48000.0]
['Germany' 30.0 54000.0]
['Spain' 38.0 61000.0]
['Germany' 40.0 63777.77777777778]
['France' 35.0 58000.0]
['Spain' 38.77777777777778 52000.0]
['France' 48.0 79000.0]
['Germany' 50.0 83000.0]
['France' 37.0 67000.0]]
第4步:解析分类数据
将标签值解析为数字
分类数据指的是含有标签值而不是数字值的变量。取值范围通常是固定的。例如 "Yes" 和 "No" 不能用于模型的数学计算,所以需要解析成数字。为实现这一功能,我们从 sklearn.preprocessing 库导入 LabelEncoder 类。1
2
3
4from sklearn.preprocessing import LabelEncoder
# 使用标签编码第0列
labelencoder_X = LabelEncoder()
X[ : , 0] = labelencoder_X.fit_transform(X[ : , 0])
打印 X 运行结果如下:1
2
3
4
5
6
7
8
9
10
11
12Step 4-1: Encoding categorical data
X
[[0 44.0 72000.0]
[2 27.0 48000.0]
[1 30.0 54000.0]
[2 38.0 61000.0]
[1 40.0 63777.77777777778]
[0 35.0 58000.0]
[2 38.77777777777778 52000.0]
[0 48.0 79000.0]
[1 50.0 83000.0]
[0 37.0 67000.0]]
创建虚拟变量
标签值解析成数字之后,有时还需要转为为one-hot编码,为实现这一功能,我们从 sklearn.preprocessing 库导入 OneHotEncoder 类。1
2
3
4
5
6from sklearn.preprocessing import OneHotEncoder
# 将标签转化为one-hot编码,categorical_features = [0]表示只编码第0列
onehotencoder = OneHotEncoder(categorical_features = [0])
X = onehotencoder.fit_transform(X).toarray()
labelencoder_Y = LabelEncoder()
Y = labelencoder_Y.fit_transform(Y)
如果不加 toarray() 的话,输出的是稀疏的存储格式,即索引加值的形式,也可以通过参数指定 sparse = False 来达到同样的效果。
分别打印 X 和 Y 运行结果如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24Step 4-2: Encoding categorical data
X
[[1.00000000e+00 0.00000000e+00 0.00000000e+00 4.40000000e+01
7.20000000e+04]
[0.00000000e+00 0.00000000e+00 1.00000000e+00 2.70000000e+01
4.80000000e+04]
[0.00000000e+00 1.00000000e+00 0.00000000e+00 3.00000000e+01
5.40000000e+04]
[0.00000000e+00 0.00000000e+00 1.00000000e+00 3.80000000e+01
6.10000000e+04]
[0.00000000e+00 1.00000000e+00 0.00000000e+00 4.00000000e+01
6.37777778e+04]
[1.00000000e+00 0.00000000e+00 0.00000000e+00 3.50000000e+01
5.80000000e+04]
[0.00000000e+00 0.00000000e+00 1.00000000e+00 3.87777778e+01
5.20000000e+04]
[1.00000000e+00 0.00000000e+00 0.00000000e+00 4.80000000e+01
7.90000000e+04]
[0.00000000e+00 1.00000000e+00 0.00000000e+00 5.00000000e+01
8.30000000e+04]
[1.00000000e+00 0.00000000e+00 0.00000000e+00 3.70000000e+01
6.70000000e+04]]
Y
[0 1 0 0 1 1 0 1 0 1]
LabelBinarizer 将上述两步合并
使用 sklearn.preprocessing 中的 LabelBinarizer 类,可以一步执行两个转换(从文本分类到整数分类,再从整数分类到独热向量)
注意运行 fit_transform() 方法后,默认返回一个密集 NumPy 数组。向构造器 LabelBinarizer 传递 sparse_output=True ,就可以得到一个稀疏矩阵。
第5步:拆分数据集为训练集合和测试集合
把数据集拆分成两个:一个是用来训练模型的训练集合,另一个是用来验证模型的测试集合。两者比例一般是 80:20 。我们导入 sklearn.model_selection 库中的 train_test_split() 方法。1
2from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split( X , Y , test_size = 0.2, random_state = 0)
分别打印 X_train X_test Y_train 和 Y_test 运行结果如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25Step 5: Splitting the datasets into training sets and Test sets
X_train
[[0.00000000e+00 1.00000000e+00 0.00000000e+00 4.00000000e+01
6.37777778e+04]
[1.00000000e+00 0.00000000e+00 0.00000000e+00 3.70000000e+01
6.70000000e+04]
[0.00000000e+00 0.00000000e+00 1.00000000e+00 2.70000000e+01
4.80000000e+04]
[0.00000000e+00 0.00000000e+00 1.00000000e+00 3.87777778e+01
5.20000000e+04]
[1.00000000e+00 0.00000000e+00 0.00000000e+00 4.80000000e+01
7.90000000e+04]
[0.00000000e+00 0.00000000e+00 1.00000000e+00 3.80000000e+01
6.10000000e+04]
[1.00000000e+00 0.00000000e+00 0.00000000e+00 4.40000000e+01
7.20000000e+04]
[1.00000000e+00 0.00000000e+00 0.00000000e+00 3.50000000e+01
5.80000000e+04]]
X_test
[[0.0e+00 1.0e+00 0.0e+00 3.0e+01 5.4e+04]
[0.0e+00 1.0e+00 0.0e+00 5.0e+01 8.3e+04]]
Y_train
[1 1 1 0 1 0 0 1]
Y_test
[0 0]
第6步:特征量化
大部分模型算法使用两点间的欧氏距离表示,但此特征在幅度、单位和范围姿态问题上变化很大。在距离计算中,高幅度的特征比低幅度特征权重更大。可用特征标准化或Z值归一化解决。导入 sklearn.preprocessing 库的 StandardScalar 类。1
2
3
4from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)
数据归一化后,打印X_train X_test 运行结果如下:1
2
3
4
5
6
7
8
9
10
11
12
13Step 6: Feature Scaling
X_train
[[-1. 2.64575131 -0.77459667 0.26306757 0.12381479]
[ 1. -0.37796447 -0.77459667 -0.25350148 0.46175632]
[-1. -0.37796447 1.29099445 -1.97539832 -1.53093341]
[-1. -0.37796447 1.29099445 0.05261351 -1.11141978]
[ 1. -0.37796447 -0.77459667 1.64058505 1.7202972 ]
[-1. -0.37796447 1.29099445 -0.0813118 -0.16751412]
[ 1. -0.37796447 -0.77459667 0.95182631 0.98614835]
[ 1. -0.37796447 -0.77459667 -0.59788085 -0.48214934]]
X_test
[[-1. 2.64575131 -0.77459667 -1.45882927 -0.90166297]
[-1. 2.64575131 -0.77459667 1.98496442 2.13981082]]
数据预处理补充
样例数据集
| sepal_length_cm | sepal_width_cm | petal_length_cm | petal_width_cm | class |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 4.9 | 3 | 1.4 | 0.2 | Iris-setosa |
| 4.7 | 3.2 | 1.3 | 0.2 | Iris-setosa |
| 4.6 | 3.1 | 1.5 | 0.2 | Iris-setosa |
| 5 | 3.6 | 1.4 | 0.2 | Iris-setosa |
| 5.4 | 3.9 | 1.7 | 0.4 | Iris-setosa |
| 4.6 | 3.4 | 1.4 | 0.3 | Iris-setosa |
| 5 | 3.4 | 1.5 | NA | Iris-setosa |
| 4.4 | 2.9 | 1.4 | NA | Iris-setosa |
| 4.9 | 3.1 | 1.5 | NA | Iris-setosa |
| 5.4 | 3.7 | 1.5 | NA | Iris-setosa |
| 4.8 | 3.4 | 1.6 | NA | Iris-setosa |
| 4.8 | 3 | 1.4 | 0.1 | Iris-setosa |
| 5.7 | 3 | 1.1 | 0.1 | Iris-setosa |
| 5.8 | 4 | 1.2 | 0.2 | Iris-setosa |
| 5.7 | 4.4 | 1.5 | 0.4 | Iris-setosa |
| 5.4 | 3.9 | 1.3 | 0.4 | Iris-setosa |
| 5.1 | 3.5 | 1.4 | 0.3 | Iris-setosa |
| 5.7 | 3.8 | 1.7 | 0.3 | Iris-setossa |
| 5.1 | 3.8 | 1.5 | 0.3 | Iris-setosa |
| 5.4 | 3.4 | 1.7 | 0.2 | Iris-setosa |
| 5.1 | 3.7 | 1.5 | 0.4 | Iris-setosa |
| 4.6 | 3.6 | 1 | 0.2 | Iris-setosa |
| 5.1 | 3.3 | 1.7 | 0.5 | Iris-setosa |
| 4.8 | 3.4 | 1.9 | 0.2 | Iris-setosa |
| 5 | 3 | 1.6 | 0.2 | Iris-setosa |
| 5 | 3.4 | 1.6 | 0.4 | Iris-setosa |
| 5.2 | 3.5 | 1.5 | 0.2 | Iris-setosa |
| 5.2 | 3.4 | 1.4 | 0.2 | Iris-setosa |
| 4.7 | 3.2 | 1.6 | 0.2 | Iris-setosa |
| 4.8 | 3.1 | 1.6 | 0.2 | Iris-setosa |
| 5.4 | 3.4 | 1.5 | 0.4 | Iris-setosa |
| 5.2 | 4.1 | 1.5 | 0.1 | Iris-setosa |
| 5.5 | 4.2 | 1.4 | 0.2 | Iris-setosa |
| 4.9 | 3.1 | 1.5 | 0.1 | Iris-setosa |
| 5 | 3.2 | 1.2 | 0.2 | Iris-setosa |
| 5.5 | 3.5 | 1.3 | 0.2 | Iris-setosa |
| 4.9 | 3.1 | 1.5 | 0.1 | Iris-setosa |
| 4.4 | 3 | 1.3 | 0.2 | Iris-setosa |
| 5.1 | 3.4 | 1.5 | 0.2 | Iris-setosa |
| 5 | 3.5 | 1.3 | 0.3 | Iris-setosa |
| 4.5 | 2.3 | 1.3 | 0.3 | Iris-setosa |
| 4.4 | 3.2 | 1.3 | 0.2 | Iris-setosa |
| 5 | 3.5 | 1.6 | 0.6 | Iris-setosa |
| 5.1 | 3.8 | 1.9 | 0.4 | Iris-setosa |
| 4.8 | 3 | 1.4 | 0.3 | Iris-setosa |
| 5.1 | 3.8 | 1.6 | 0.2 | Iris-setosa |
| 4.6 | 3.2 | 1.4 | 0.2 | Iris-setosa |
| 5.3 | 3.7 | 1.5 | 0.2 | Iris-setosa |
| 5 | 3.3 | 1.4 | 0.2 | Iris-setosa |
| 7 | 3.2 | 4.7 | 1.4 | Iris-versicolor |
| 6.4 | 3.2 | 4.5 | 1.5 | Iris-versicolor |
| 6.9 | 3.1 | 4.9 | 1.5 | Iris-versicolor |
| 5.5 | 2.3 | 4 | 1.3 | Iris-versicolor |
| 6.5 | 2.8 | 4.6 | 1.5 | Iris-versicolor |
| 5.7 | 2.8 | 4.5 | 1.3 | Iris-versicolor |
| 6.3 | 3.3 | 4.7 | 1.6 | Iris-versicolor |
| 4.9 | 2.4 | 3.3 | 1 | Iris-versicolor |
| 6.6 | 2.9 | 4.6 | 1.3 | Iris-versicolor |
| 5.2 | 2.7 | 3.9 | 1.4 | Iris-versicolor |
| 5 | 2 | 3.5 | 1 | Iris-versicolor |
| 5.9 | 3 | 4.2 | 1.5 | Iris-versicolor |
| 6 | 2.2 | 4 | 1 | Iris-versicolor |
| 6.1 | 2.9 | 4.7 | 1.4 | Iris-versicolor |
| 5.6 | 2.9 | 3.6 | 1.3 | Iris-versicolor |
| 6.7 | 3.1 | 4.4 | 1.4 | Iris-versicolor |
| 5.6 | 3 | 4.5 | 1.5 | Iris-versicolor |
| 5.8 | 2.7 | 4.1 | 1 | Iris-versicolor |
| 6.2 | 2.2 | 4.5 | 1.5 | Iris-versicolor |
| 5.6 | 2.5 | 3.9 | 1.1 | Iris-versicolor |
| 5.9 | 3.2 | 4.8 | 1.8 | Iris-versicolor |
| 6.1 | 2.8 | 4 | 1.3 | Iris-versicolor |
| 6.3 | 2.5 | 4.9 | 1.5 | Iris-versicolor |
| 6.1 | 2.8 | 4.7 | 1.2 | Iris-versicolor |
| 6.4 | 2.9 | 4.3 | 1.3 | Iris-versicolor |
| 6.6 | 3 | 4.4 | 1.4 | Iris-versicolor |
| 6.8 | 2.8 | 4.8 | 1.4 | Iris-versicolor |
| 0.067 | 3 | 5 | 1.7 | Iris-versicolor |
| 0.06 | 2.9 | 4.5 | 1.5 | Iris-versicolor |
| 0.057 | 2.6 | 3.5 | 1 | Iris-versicolor |
| 0.055 | 2.4 | 3.8 | 1.1 | Iris-versicolor |
| 0.055 | 2.4 | 3.7 | 1 | Iris-versicolor |
| 5.8 | 2.7 | 3.9 | 1.2 | Iris-versicolor |
| 6 | 2.8 | 5.1 | 1.6 | Iris-versicolor |
| 5.4 | 3 | 4.5 | 1.5 | Iris-versicolor |
| 6 | 3.4 | 4.5 | 1.6 | Iris-versicolor |
| 6.7 | 3.1 | 4.7 | 1.5 | Iris-versicolor |
| 6.3 | 2.3 | 4.4 | 1.3 | Iris-versicolor |
| 5.6 | 3 | 4.1 | 1.3 | Iris-versicolor |
| 5.5 | 2.5 | 4 | 1.3 | Iris-versicolor |
| 5.5 | 2.6 | 4.4 | 1.2 | Iris-versicolor |
| 6.1 | 3 | 4.6 | 1.4 | Iris-versicolor |
| 5.8 | 2.6 | 4 | 1.2 | Iris-versicolor |
| 5 | 2.3 | 3.3 | 1 | Iris-versicolor |
| 5.6 | 2.7 | 4.2 | 1.3 | Iris-versicolor |
| 5.7 | 3 | 4.2 | 1.2 | versicolor |
| 5.7 | 2.9 | 4.2 | 1.3 | versicolor |
| 6.2 | 2.9 | 4.3 | 1.3 | versicolor |
| 5.1 | 2.5 | 3 | 1.1 | versicolor |
| 5.7 | 2.8 | 4.1 | 1.3 | versicolor |
| 6.3 | 3.3 | 6 | 2.5 | Iris-virginica |
| 5.8 | 2.7 | 5.1 | 1.9 | Iris-virginica |
| 7.1 | 3 | 5.9 | 2.1 | Iris-virginica |
| 6.3 | 2.9 | 5.6 | 1.8 | Iris-virginica |
| 6.5 | 3 | 5.8 | 2.2 | Iris-virginica |
| 7.6 | 3 | 6.6 | 2.1 | Iris-virginica |
| 4.9 | 2.5 | 4.5 | 1.7 | Iris-virginica |
| 7.3 | 2.9 | 6.3 | 1.8 | Iris-virginica |
| 6.7 | 2.5 | 5.8 | 1.8 | Iris-virginica |
| 7.2 | 3.6 | 6.1 | 2.5 | Iris-virginica |
| 6.5 | 3.2 | 5.1 | 2 | Iris-virginica |
| 6.4 | 2.7 | 5.3 | 1.9 | Iris-virginica |
| 6.8 | 3 | 5.5 | 2.1 | Iris-virginica |
| 5.7 | 2.5 | 5 | 2 | Iris-virginica |
| 5.8 | 2.8 | 5.1 | 2.4 | Iris-virginica |
| 6.4 | 3.2 | 5.3 | 2.3 | Iris-virginica |
| 6.5 | 3 | 5.5 | 1.8 | Iris-virginica |
| 7.7 | 3.8 | 6.7 | 2.2 | Iris-virginica |
| 7.7 | 2.6 | 6.9 | 2.3 | Iris-virginica |
| 6 | 2.2 | 5 | 1.5 | Iris-virginica |
| 6.9 | 3.2 | 5.7 | 2.3 | Iris-virginica |
| 5.6 | 2.8 | 4.9 | 2 | Iris-virginica |
| 5.6 | 2.8 | 6.7 | 2 | Iris-virginica |
| 6.3 | 2.7 | 4.9 | 1.8 | Iris-virginica |
| 6.7 | 3.3 | 5.7 | 2.1 | Iris-virginica |
| 7.2 | 3.2 | 6 | 1.8 | Iris-virginica |
| 6.2 | 2.8 | 4.8 | 1.8 | Iris-virginica |
| 6.1 | 3 | 4.9 | 1.8 | Iris-virginica |
| 6.4 | 2.8 | 5.6 | 2.1 | Iris-virginica |
| 7.2 | 3 | 5.8 | 1.6 | Iris-virginica |
| 7.4 | 2.8 | 6.1 | 1.9 | Iris-virginica |
| 7.9 | 3.8 | 6.4 | 2 | Iris-virginica |
| 6.4 | 2.8 | 5.6 | 2.2 | Iris-virginica |
| 6.3 | 2.8 | 5.1 | 1.5 | Iris-virginica |
| 6.1 | 2.6 | 5.6 | 1.4 | Iris-virginica |
| 7.7 | 3 | 6.1 | 2.3 | Iris-virginica |
| 6.3 | 3.4 | 5.6 | 2.4 | Iris-virginica |
| 6.4 | 3.1 | 5.5 | 1.8 | Iris-virginica |
| 6 | 3 | 4.8 | 1.8 | Iris-virginica |
| 6.9 | 3.1 | 5.4 | 2.1 | Iris-virginica |
| 6.7 | 3.1 | 5.6 | 2.4 | Iris-virginica |
| 6.9 | 3.1 | 5.1 | 2.3 | Iris-virginica |
| 5.8 | 2.7 | 5.1 | 1.9 | Iris-virginica |
| 6.8 | 3.2 | 5.9 | 2.3 | Iris-virginica |
| 6.7 | 3.3 | 5.7 | 2.5 | Iris-virginica |
| 6.7 | 3 | 5.2 | 2.3 | Iris-virginica |
| 6.3 | 2.5 | 5 | 2.3 | Iris-virginica |
| 6.5 | 3 | 5.2 | 2 | Iris-virginica |
| 6.2 | 3.4 | 5.4 | 2.3 | Iris-virginica |
| 5.9 | 3 | 5.1 | 1.8 | Iris-virginica |
获取数据集基本信息
导入数据集
1 | import pandas as pd |
获取表头信息
1 | df.head() |
输出结果:1
2
3
4
5
6
7
8
9
10
11
12
13 sepal_length_cm sepal_width_cm petal_length_cm petal_width_cm \
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
class
0 Iris-setosa
1 Iris-setosa
2 Iris-setosa
3 Iris-setosa
4 Iris-setosa
获取每列特征的指标:个数 均值 标准差 最小值 分位数 最大值
1 | df.describe() # 可传入参数 include='all' 显示完整信息 |
输出结果:1
2
3
4
5
6
7
8
9 sepal_length_cm sepal_width_cm petal_length_cm petal_width_cm
count 150.000000 150.000000 150.000000 145.000000
mean 5.644627 3.054667 3.758667 1.236552
std 1.312781 0.433123 1.764420 0.755058
min 0.055000 2.000000 1.000000 0.100000
25% 5.100000 2.800000 1.600000 0.400000
50% 5.700000 3.000000 4.350000 1.300000
75% 6.400000 3.300000 5.100000 1.800000
max 7.900000 4.400000 6.900000 2.500000
获取pandas类基础信息
1 | df.info() |
输出结果:1
2
3
4
5
6
7
8
9
10<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 5 columns):
sepal_length_cm 150 non-null float64
sepal_width_cm 150 non-null float64
petal_length_cm 150 non-null float64
petal_width_cm 145 non-null float64
class 150 non-null object
dtypes: float64(4), object(1)
memory usage: 5.9+ KB
删除无效数据
从上面输出的信息可以看到,属性 petal_width_cm 有 5 个缺失值,因为数据量不大,这里未做填充处理,直接删除 5 条数据。1
df = df.dropna(subset=['petal_width_cm'])
Pairplot多变量图 ★
当处理多维特征时(三维以上),由于图像化只能是平面,难以将高位特征图像化,但是我们可以将特征进行两两对比,分别作图,分析两两特征之间的关系。这里我们用到 seaborn 中的 pairplot 函数1
2
3
4import matplotlib.pyplot as plt
import seaborn as sns
sns.pairplot(df, hue='class', diag_kind='hist', size=2.5)
plt.show()
运行结果如下图: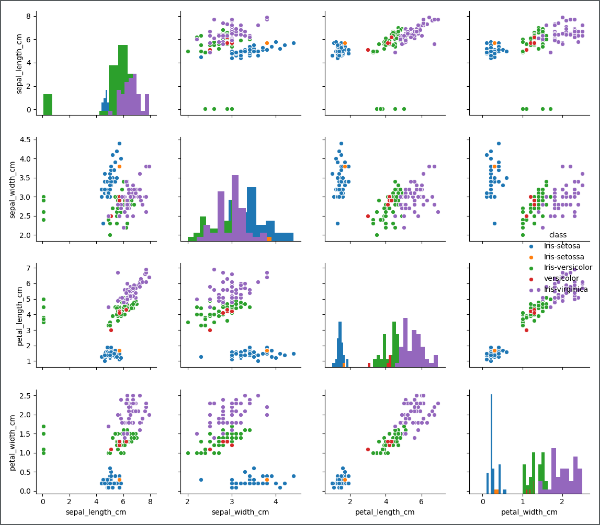
函数说明:
seaborn.pairplot(data, hue=None, hue_order=None, palette=None, vars=None, x_vars=None, y_vars=None, kind='scatter', diag_kind='hist', markers=None, size=2.5, aspect=1, dropna=True, plot_kws=None, diag_kws=None, grid_kws=None)¶
参数说明:
data: DataFrame,需要分析的数据集,每一行为一个观测数据,每一列为一个变量hue: string (variable name), optional,数据集的类别的列名hue_order: list of strings,palette: dict or seaborn color palette,调色板颜色vars: list of variable names, optional,变量,否则使用data的全部变量{x, y}_vars: lists of variable names, optional,x变量和y变量,否则使用data的全部变量kind: {‘scatter’, ‘reg’}, optional,非对角线关系图的类型- diag_kind` : {‘auto’, ‘hist’, ‘kde’}, optional,主对角线关系图的类型
markers: single matplotlib marker code or list, optional,使用不同的形状。”o”:圆,”s”:方块,”D”:菱形height: scalar, optional,调整画布大小size: 默认 2.5,图的尺度大小(正方形)aspect: scalar, optional,dropna: boolean, optional,是否剔除缺失值{plot, diag, grid}_kws: dicts, optional,
异常值检查
类名错误
从上图从我们可以观察到一些分类名字的异常,比如橙色的点仅有一个(混在蓝色数据中),红色的点也比较少(混在绿色数据中)。似乎橙色点和红色点是异常点,我们看一下类别的名字,做进一步分析。1
df['class'].value_counts()
输出结果如下:1
2
3
4
5
6Iris-virginica 50
Iris-versicolor 45
Iris-setosa 44
versicolor 5
Iris-setossa 1
Name: class, dtype: int64
明显有最下面的两个类别应该归并到上面:
- 5 个数据点
versicolor应该属于Iris-versicolor - 1 个数据点
Iris-setossa应该属于Iris-setosa
运行如下代码进行调整:1
df['class'].replace(["Iris-setossa","versicolor"], ["Iris-setosa","Iris-versicolor"], inplace=True)
数据单位错误
从上图的第一行、第一列的图中可以看到,绿色的类别中,总有 5 个数据远离绿色数据整体分布,因为绿色点异常点出现在第一行、第一列的图中,对应的特征变量值为 sepal_length_cm ,我们将特征变量单独拿出来分析:1
2df.hist(column='sepal_length_cm', bins=20, figsize=(10,5))
plt.show()
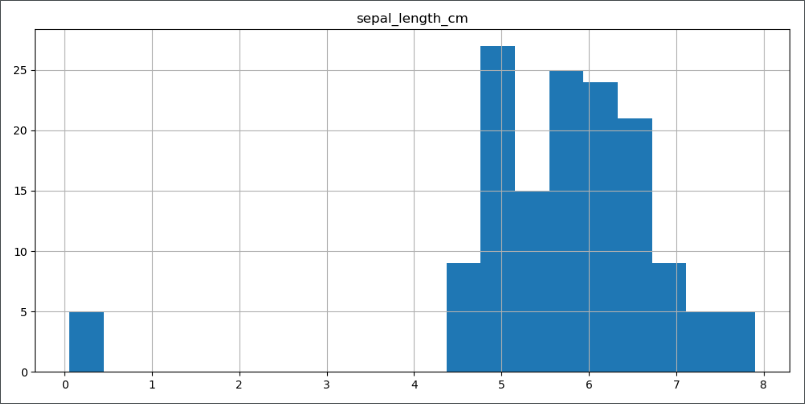
从上图可以明确的看到,有 5 个异常点的值小于 1,远远小于其他数据点,进一步分析发现,异常点的单位为 m,而正常点单位为 cm,所以做如下修改:1
2
3df.loc[df.sepal_length_cm < 1, ['sepal_length_cm']] = df['sepal_length_cm']*100
df.hist(column='sepal_length_cm', bins=20, figsize=(10, 5))
plt.show()
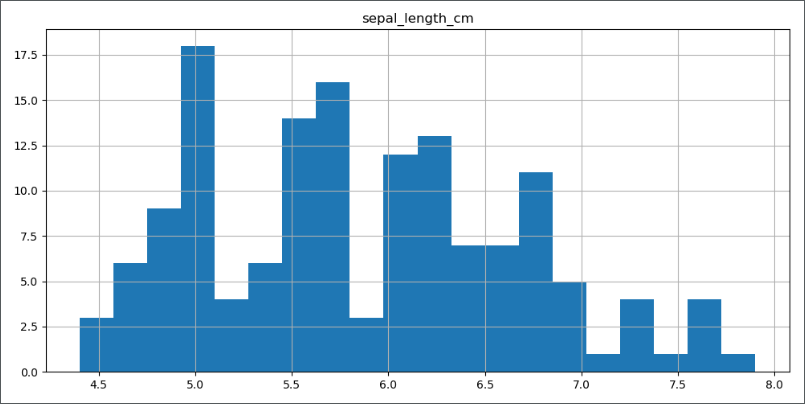
观察分布图,异常值回复正常。我们最后在看一下多变量图的变化: