支持向量机 SVM 算法实战

线性可分 SVM

导入包

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm

支持向量机的内置算法主要封装在 sklearn 中，直接导入 svm 即可。

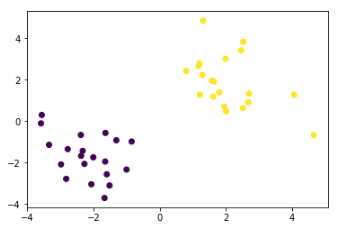
生成样本数据

# 创建40个点
x_data = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
y_data = [0]*20 +[1]*20
# 绘制图形
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
plt.show()

np.r_ 函数用于按列链接两个矩阵，绘制数据图如下：

训练模型

# fit the model
model = svm.SVC(kernel='linear')
model.fit(x_data, y_data)

直接掉包，训练过程非常简单，输出为：

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=’ovr’, degree=3, gamma=’auto’, kernel=’linear’,
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)

输出模型训练好的参数

model.coef_
model.intercept_

coef 为权值， intercept 为偏置值，输出结果如下：

array([[0.46732084, 0.45985473]])
array([-0.15579273])

画出分离平面

# 获取分离平面 
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
x_test = np.array([[-5],[5]])
d = -model.intercept_/model.coef_[0][1]
k = -model.coef_[0][0]/model.coef_[0][1]
y_test = d + k*x_test
plt.plot(x_test, y_test, 'k')
plt.show()

运行结果如下图：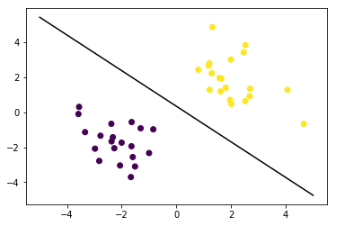

输出支持向量

model.support_vectors_

输出结果如下：

array([[-0.84486093, -0.97715396],
[ 2.00694095, 0.47369914],
[ 1.2155688 , 1.27816325]])

画出间隔边界

# 画出通过支持向量的分界线
b1 = model.support_vectors_[0]
y_down = k*x_test + (b1[1] - k*b1[0])
b2 = model.support_vectors_[-1]
y_up = k*x_test + (b2[1] - k*b2[0])
# 绘图
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
x_test = np.array([[-5],[5]])
d = -model.intercept_/model.coef_[0][1]
k = -model.coef_[0][0]/model.coef_[0][1]
y_test = d + k*x_test
plt.plot(x_test, y_test, 'k')
plt.plot(x_test, y_down, 'r--')
plt.plot(x_test, y_up, 'b--')
plt.show()

运行结果如下图：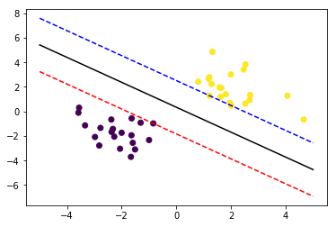

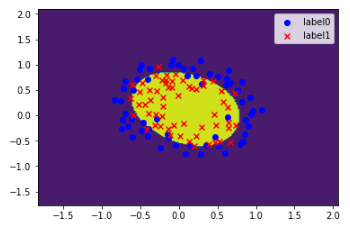
非线性可分 SVM

导入包

导入包

import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import svm

载入数据

# 载入数据
data = np.genfromtxt("LR-testSet2.txt", delimiter=",")
x_data = data[:,:-1]
y_data = data[:,-1]
    
def plot():
    x0 = []
    x1 = []
    y0 = []
    y1 = []
    # 切分不同类别的数据
    for i in range(len(x_data)):
        if y_data[i]==0:
            x0.append(x_data[i,0])
            y0.append(x_data[i,1])
        else:
            x1.append(x_data[i,0])
            y1.append(x_data[i,1])

    # 画图
    scatter0 = plt.scatter(x0, y0, c='b', marker='o')
    scatter1 = plt.scatter(x1, y1, c='r', marker='x')
    #画图例
    plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')
    
plot()
plt.show()

运行结果如下图：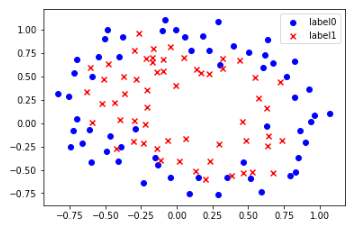

训练模型

# fit the model
# C和gamma
# 'linear', 'poly', 'rbf', 'sigmoid', 'precomputed'
model = svm.SVC(kernel='rbf', C=2, gamma=1)
model.fit(x_data, y_data)

kernel 有 5 个参数可选，分别对应不同的核函数： 'linear', 'poly', 'rbf', 'sigmoid', 'precomputed' 。 C 和 gamma 对应两个超参数，可以调整使得准确率最优。

获得模型准确率

model.score(x_data,y_data)

输出结果为：

0.847457627118644

画出决策边界

# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1

# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

z = model.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据
z = z.reshape(xx.shape)

# 等高线图
cs = plt.contourf(xx, yy, z)
plot() 
plt.show()

代码运行结果如下图：

人脸识别