SVM 概述
SVM 诞生于上世纪九十年代,由于它良好的性能,自一诞生便席卷了机器学习领域,并牢牢压制了神经网络领域好多年,据说 LeNet5(一种 CNN 手写数字识别算法,属于神经网络)自 1998 年诞生,在后来的好长一段时间并未能火起来,最主要的原因就是 SVM 这货,因为 SVM 也能达到类似的效果甚至超过 LeNet5, 而且比 LeNet5 计算量小。在不考虑集成学习和特定场景情况下,在分类算法中 SVM 毫无疑问是性能最好的分类器。下面就 SVM 的算法原理做一下总结和探讨。
SVM 的基本形式是一个有监督的线性二分类模型,它是间隔最大化的分类器。主要包括以下几种形式:
- 当训练数据线性可分时,支持向量机通过硬间隔最大化学习分类器,称为硬间隔支持向量机;
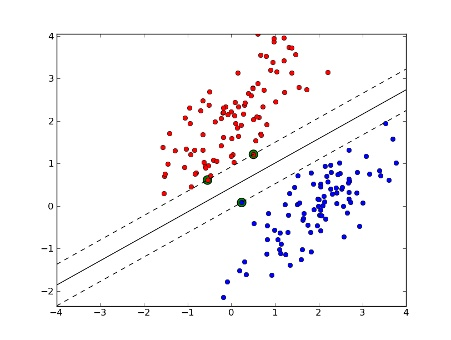
- 当训练数据近似线性可分时,支持向量机通过软间隔最大化学习分类器,称为软间隔支持向量机;
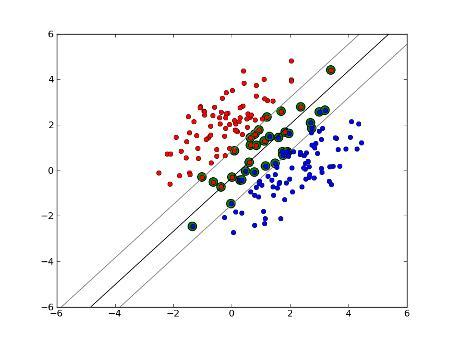
- 当训练数据线性不可分时,支持向量机通过核技巧和软间隔最大化学习分类器,称为非线性支持向量机;
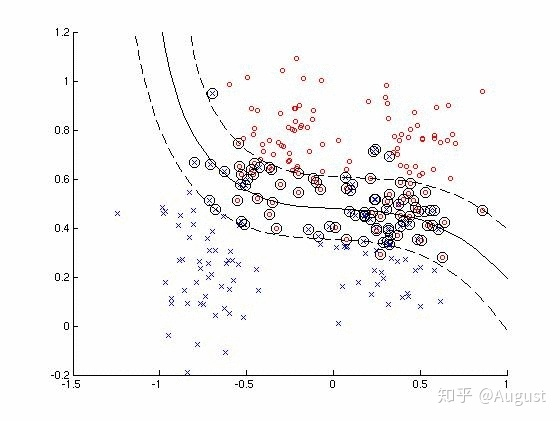
此外,SVM 既支持二元分类也支持多元分类,既支持分类问题也支持回归问题。
线性可分支持向量机
函数间隔与几何间隔
凸优化问题
- 无约束优化问题(费马定理):
$$\min f(x)$$ - 带等式约束的优化问题(拉格朗日乘子法):
$$\begin{array}{c}{\min f(x)} \\ {\text { s.t. } h_{i}(x)=0, \quad i=1,2, \cdots n} \\ \mathcal{L}(x, \lambda)=f(x)+\sum_{i=1}^{n} \lambda_{i} h_{i}(x) \end{array}$$ - 带不等式约束的优化问题(KKT条件):
$$\begin{array}{c}{\min f(x)} \\ {\text {s.t.} h_{i}(x)=0, \quad i=1,2, \cdots, n} \\ {g_{i}(x) \leq 0, \quad i=1,2, \cdots, k} \\ \mathcal{L}(x, \lambda, v)=f(x)+\sum_{i=1}^{k} \lambda_{i} g_{i}(x)+\sum_{i=1}^{n} v_{i} h_{i}(x) \end{array}$$
对偶问题
序列最小化 SMO 算法
软间隔支持向量机
线性分类 SVM 面临的问题
在节中,我们对线性可分 SVM 的算法的原理和流程进行了总结,如下图所示,为线性可分的数据集,我们可以采用线性可分的支持向量机,也称为硬间隔支持向量机。
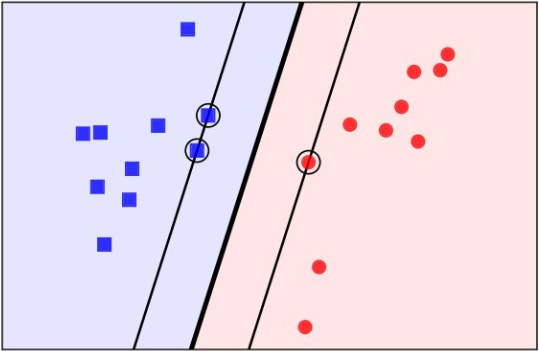
当数据集中参杂了一些噪声,如下图所示,由于参杂了一个红色的噪声点,导致模型学习到的决策边界由下图中的粗虚线移动到了粗实线。
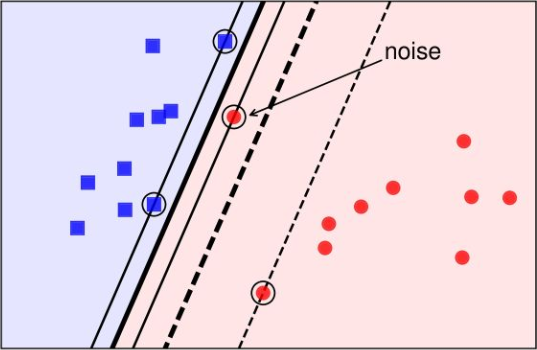
上图是粗实线作为决策边界更合理,还是粗虚线作为决策边界更合理?很显然是粗虚线更合理,因为粗虚线忽略了噪音的影响,其 margin 更大,在测试集上的效果要优于粗实线。
如何解决这些问题呢? SVM 引入了软间隔最大化的方法来解决。
硬间隔 SVM 回顾
回顾下最大硬间隔的 SVM:
$$\min \frac{1}{2}|w|_ {2}^{2} \quad \text { s.t } y_{i}\left(w^{T} x_{i}+b\right) \geq 1(i=1,2, \ldots m)$$
硬间隔支持向量机,如下图所示:
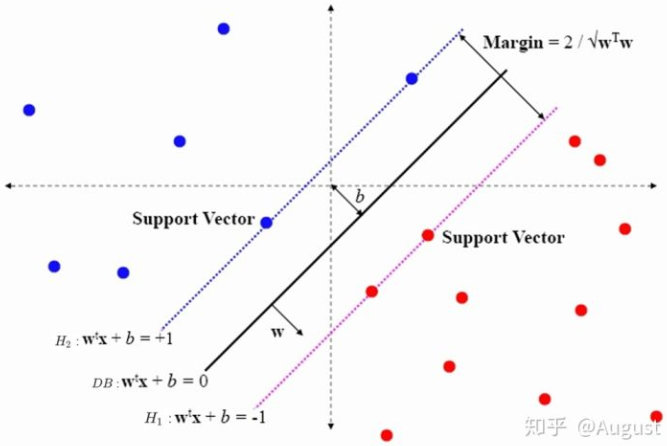
所有的样本点均到决策超平面的距离均不小于 1,硬间隔 SVM 的下限为:
$$y_{i}\left(w^{T} x_{i}+b\right) \geq 1$$
$H_1$ 和 $H_2$ 像两堵墙一样将两类样本分隔开。
引入松弛变量 $\xi$
当数据中增加噪声点或误分类以后,比如在 $H_1$ 和 $H_2$ 之间,SVM 引入了一个神奇的变量 $\xi_i \ge 0$ ,这个变量被称为松弛变量,其几何含义由下图所示:
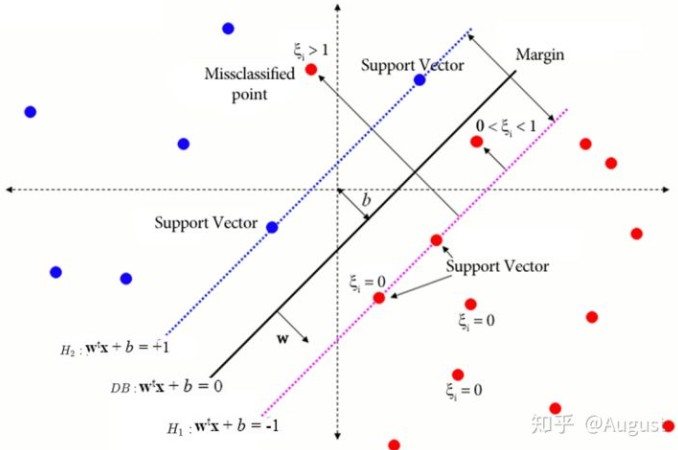
简单明了,以红点样本为例,$\xi$ 表示到 $H_1$ 的距离:
当样本点在 $H_1$ 右边时,包括支持向量和支持向量以外的样本点时 $\xi_i = 0$ ,即我们可以按照硬间隔来处理。
对于 $H_1$ 左侧的样本点,样本的 $\xi > 0$ ,包括两种情况,一种是正确分类,但是在 margin 范围内的样本点 (也就是超平面附近的点),此时 $0< \xi < 1$;一类是误分类的点,此时 $\xi >1$
$1-\xi$ 的几何含义
对于噪声点和误分类的样本点来说,$1-\xi$ 表示该样本点到决策超平面之间的距离,而且是有向距离。具体而言,噪声点到超平面的距离为 $0<1-\xi<1$,误分类点到超平面的距离为 $1-\xi<0$ 。
加入松弛变量 $\xi$ 之后,我们的 $H_1$ 和 $H_2$ 像弹簧一样,针对不同的样本点做不同的处理,变 “软”了。写成数学公式为:
$$y_{i}\left(w^{T} x_{i}+b\right) \geq 1-\xi_{i}, \quad \xi_{i} \geq 0$$
上式即为软间隔支持向量机的约束条件。
优化下界
我们知道,只要我们拉伸弹簧,我们就会消耗能量,付出代价。同理松弛变量的添加也是有成本的,每一个松弛变量 $\xi_i$ 都支付了一个代价 $\xi_i$, 现在代价函数变成了:
$$\min \frac{1}{2}|w|_ {2}^{2} \Rightarrow \min \frac{1}{2}|w|_ {2}^{2}+C \sum_{i=1}^{m} \xi_{i}$$
这个公式的原理还是不够明了,让我们还原一下,看看这个到底是什么个意思。
$$\min \frac{1}{2}|w|_ {2}^{2} \Rightarrow \max \frac{2}{|w|_ {2}^{2}}$$
$$\min \frac{C}{m} \sum_{i=1}^{m} \xi_{i} \Rightarrow \max \frac{C}{m} \sum_{i=1}^{m}\left(1-\xi_{i}\right)$$
显然对于支持向量和支持向量以外的点, $max\; \frac{2}{||w||_ 2^2}$ ,相当于最大化 margin 。
$max\;\frac C m\sum\limits_{i=1}^{m}(1-\xi_i)$ 对于 margin 内的噪声点,最大化噪声点和决策边界之间的距离$1-\xi_i$;对于误分类的点,其到决策边界之间的距离为 $-(1-\xi_i)$,那么 $max\;\;C\sum\limits_{i=1}^{m}(1-\xi_i)\Rightarrow min\;\;|C\sum\limits_{i=1}^{m}(1-\xi_i)|$ ,也就是最小化误分类点到决策边界之间的距离,翻译成汉语就是让其尽量不要错得那么离谱。
软间隔 SVM 的优化目标
综合起来,我们就得到了最大软间隔 SVM 的优化目标:
$$ \begin{array}{c}{\min \frac{1}{2}|w|_ {2}^{2}+\frac{C}{m} \sum_{i=1}^{m} \xi_{i}} \\ {\text {s.t. } y_{i}\left(w^{T} x_{i}+b\right) \geq 1-\xi_{i} \quad(i=1,2, \ldots m)} \\ {\xi_{i} \geq 0 \quad(i=1,2, \ldots m)}\end{array} $$
最小化 $\frac{1}{2}||w||_ 2^2$ 意味着让支持向量距离超平面的距离尽可能大,最小化 $\sum\limits_{i=1}^{m}\xi_i $ 意味着保证 margin 内的点尽可能远离超平面,对误分类的点不要偏离的太远。$C$ 是协调两者关系的系数,需要调参来选择。
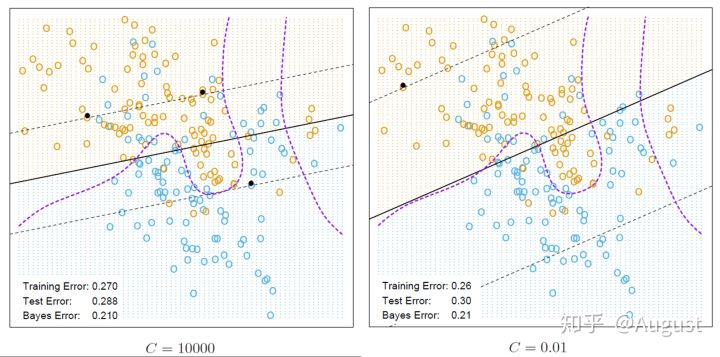
下面是取不同的 $C$ 值的分类器对比情况,这两种分类器的性能相差不大,都比较差。$C$ 越小,margin 越大,$C$ 越大,margin 越小。$C$ 越大,$\sum\limits_{i=1}^{m}\xi_i$ 作用越大,模型会更多得关注噪声点和误分类点,即决策边界周围的点,$C$ 越小,模型会更多关注距离决策边界更远的点,当 $C=0$ 时,软间隔变成了硬间隔。 $C$ 的取值可以采用交叉验证的方式求得。
SVM 损失函数
总结一下,关于线性支持向量机我们学了三种代价函数:
- 合页损失函数 (hinge loss function):
$$\min \frac{1}{m} \sum_{i=1}^{m} \max {0,1-y_{i}(w^{T} x_{i}+b)}+\frac{\lambda}{2}|w|_ {2}^{2}$$ - 硬间隔损失函数:
$$\min \frac{1}{2}|w|_ {2}^{2} \quad \text { s.t } y_{i}\left(w^{T} x_{i}+b\right) \geq 1(i=1,2, \ldots m)$$ - 软间隔损失函数:
$$\begin{array}{c}{\min \frac{1}{2}|w|_ {2}^{2}+\frac{C}{m} \sum_{i=1}^{m} \xi_{i}} \\\\ {\text {s.t. } y_{i}\left(w^{T} x_{i}+b\right) \geq 1-\xi_{i} \quad(i=1,2, \ldots m)} \\\\ {\xi_{i} \geq 0(i=1,2, \ldots m)}\end{array}$$
其实归根到底都是合页损失函数。
推导以后补充
非线性支持向量机与核函数
以上介绍的都是 SVM 作为线性分类器的作用,那对于非线性问题,SVM 该怎样做呢?
对于非线性问题,我们采取的做法是将进行一个非线性变换映射到特征空间中,将原空间非线性问题转变为特征空间的线性问题,然后再用线性分类器 SVM 求解。什么意思呢?我们举例说明:

图中的两类数据,分别分布为两个圆圈的形状,因为这样的数据本身就是线性不可分的,线性分类器是没法处理。那我们该如何处理呢?
对于上图的数据,我们可以表示为:
$$a_{1} X_{1}^{2}+a_{2}\left(X_{2}-c\right)^{2}+a_{3}=0$$
其中 $X_1$ 和 $X_2$ 是两个坐标系。
我们令 $Z_1=X^2_1, Z_2=X^2_2, Z_3=X_2$ (其中 $Z_1, Z_2, Z_3$ 为三维空间的三个坐标)将其映射到三维空间中进行求解,如下图:

可以找到一个平面,将红色的样本和蓝色样本区分开。
下面展示了另一种特征映射和线性分类相结合的方式: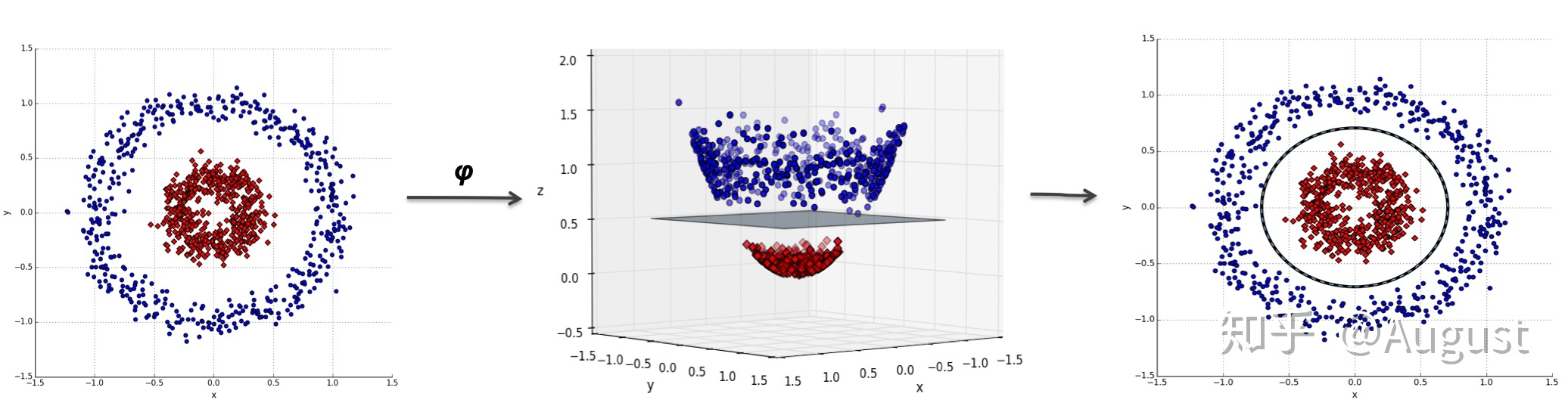
也就是说对于在低维线性不可分的数据,在映射到了高维以后,就变成线性可分的了。这个思想我们同样可以运用到 SVM 的线性不可分数据上。也就是说,对于 SVM 线性不可分的低维特征数据,我们可以将其映射到高维,就可以运用线性可分 SVM 的进行求解了。
核函数的引入
核函数的定义
假设 $\phi$ 是一个从低维的输入空间 $\chi$(欧式空间的子集或者离散集合)到高维的希尔伯特空间的 $H$ 映射。对于所有的 $x, z \in \chi$,都有 $K(x, z)$ 满足:
$$K(x, z)=\phi(x) \cdot \phi(z)$$
那么我们就称 $K(x, z)$ 为核函数,$\phi(x)$ 为映射函数 。式中 $\phi(x) \cdot \phi(z)$ 为 $\phi(x)$ 和 $\phi(z)$ 的内积。
核技巧在支持向量机中的应用
回顾线性可分 SVM 对偶问题的优化目标函数:
$$\underbrace{\min }_ {\alpha} \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{m} \alpha_{i} \\\\ {\quad \text {s.t.} \sum_{i=1}^{m} \alpha_{i} y_{i}=0} \\\\ {0 \leq \alpha_{i} \leq C ,i=1,2, \ldots m}$$
我们定义一个低维特征空间到高维特征空间的映射 $\phi$,将所有输入空间映射到一个更高维度的特征空间,让数据线性可分,我们就可以利用 SVM 的优化目标函数求出分类决策边界了。也就是说现在的 SVM 的优化目标函数变成:
$$\underbrace{\min }_ {\alpha} \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j}[\phi(x_{i}) \cdot \phi(x_{j})]-\sum_{i=1}^{m} \alpha_{i}$$
上式 $\phi(x_{i}) \cdot \phi(x_{j})$ 替换为核函数:
$$\underbrace{\min }_ {\alpha} \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j}K(x_i, x_j)-\sum_{i=1}^{m} \alpha_{i}$$
同样,分类决策函数中的内积也可以用核函数代替,得到的超平面即为:
$$f(x)={sign}\left(\sum_{i=1}^{m} \alpha_{i}^{\ast} y_{i}\left(\phi\left(x_{i}\right) \cdot \phi(x)\right)+b^{\ast}\right) = {sign}\left(\sum_{i=1}^{m} \alpha_{i}^{\ast} y_{i}K(x_i, x_j)+b^{\ast}\right) $$
核函数介绍
从上面的分析发现,因此我们只需要定义核函数 $K(x,z)$,而不用显示的定义映射函数 $\phi$ ,即可求出 $\phi(x_i) \cdot \phi(x_j)$, 这样就省去了寻找映射函数的麻烦(映射函数有无数个)。但是却带来了另一个问题:我们怎样定义核函数 $K(x,z)$ 呢?
其实已经有人帮我们找到了很多的核函数,而且常用的核函数也仅仅只有那么几个。下面我们简要介绍 sklearn 中默认可选的几个核函数。
线性核函数
线性核函数(Linear Kernel)其实就是线性可分 SVM,表达式为:
$$K(x, z)=x \cdot z$$
也就是说,线性 SVM 是非线性 SVM 的一个特殊的情况,即线性 SVM 是使用线性核函数的 SVM。
多项式核函数
多项式核函数(Polynomial Kernel)是线性不可分SVM常用的核函数之一,表达式为:
$$ K(x, z)=(\gamma x \bullet z+r)^{d} $$
其中,$\gamma,r,d$ 都需要自己调参定义。
高斯核函数
高斯核函数(Gaussian Kernel),在SVM中也称为径向基核函数(Radial Basis Function,RBF),它是非线性分类SVM最主流的核函数。表达式为:
$$ K(x, z)=\exp \left(-\gamma|x-z|^{2}\right) $$
其中,$\gamma$ 大于 0,需要自己调参定义。
拉普拉斯核函数
$$ K(x, z)=\exp \left(-\gamma|x-z|\right) $$
Sigmoid核函数
Sigmoid 核函数(Sigmoid Kernel)也是线性不可分SVM常用的核函数之一,表达式为:
$$ K(x, z)=\tanh (\gamma x \bullet z+r) $$
其中,$\gamma, r$ 都需要自己调参定义。
