数据结构与算法笔记 (三)

位运算

什么是位运算

程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。比如，and 运算本来是一个逻辑运算符，但整数与整数之间也可以进行and 运算。举个例子，6 的二进制是 110，11 的二进制是 1011，那么 6 and 11 的结果就是 2，它是二进制对应位进行逻辑运算的结果（0 表示 False，1 表示 True，空位都当 0 处理）。

由于位运算直接对内存数据进行操作，不需要转成十进制，因此处理速度非常快。

常见的位运算符

符号	描述	运算规则
&	与	两个位都为 1 时，结果才为 1
︱	或	两个位都为 0 时，结果才为 0
^	异或	两个位相同为 0，相异为 1
~	取反	0 变 1，1 变 0
<<	左移	各二进位全部左移若干位，高位丢弃，低位补0
>>	右移	各二进位全部右移若干位，对无符号数，高位补0，有符号数，各编译器处理方法不一样，有的补符号位（算术右移），有的补0（逻辑右移）

XOR - 异或

异或：相同为 0 ，不同为 1 。也可用「不进位加法」来理解。

异或操作的一些特点：

x ^ 0 = x
x ^ 1s = ~x // 1s = ~0
x ^ (~x) = 1s
x ^ x = 0 // interesting and important!
a ^ b = c => a ^ c = b, b ^ c = a // swap
a ^ b ^ c = a ^ (b ^ c) = (a ^ b) ^ c // associative

实战常用的位运算操作：

X & 1 == 1 OR == 0 判断奇偶（x % 2 == 1）
X = X & (X - 1) => 清零最低位的 1
X & -X => X 为偶数得到最低位的 1（或结果为能被这个数整除的最大2的次幂），X 是奇数，则结果必为 1

更为复杂的位运算操作：

将 x 最右边的 n 位清零 - x & (~0 << n)
获取 x 的第 n 位值（0 或者 1）- (x >> n) & 1
获取 x 的第 n 位的幂值 - x & (1 << (n - 1))
仅将第 n 位置为 1 - x | (1 << n)
仅将第 n 位置为 0 - x & (~(1 << n))
将 x 最高位至第 n 位（含）清零 - x & ((1 << n) - 1)
将第 n 位至第 0 位（含）清零 - x & (~((1 << (n + 1)) - 1))

代码实战

问题一位1的个数（191）

问题描述

编写一个函数，输入是一个无符号整数，返回其二进制表达式中数字位数为 1 的个数（也被称为汉明重量。

示例 1：

输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 **00000000000000000000000000001011** 中，共有三位为 '1'。

示例 2：

输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 ‘1’。

示例 3：

输入：11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 ‘1’。

提示：

请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的 示例 3 中，输入表示有符号整数 -3。

解题思路分析

方法一，x % 2 → count++; x = x >> 1，时间复杂度为存储单元的位数(32)
方法二，x = x & (x-1)，时间复杂度为 1 的个数

解法代码

Java代码

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int res = 0;
        for (; n != 0; n &= n-1)
            ++ res;
        return res;
    }
}

Python代码

class Solution(object):
    def hammingWeight(self, n):
        count = 0
        while n:
            n = n & (n - 1)
            count += 1
        return count

问题二 2的幂（231）

问题描述

给定一个整数，编写一个函数来判断它是否是 2 的幂次方。

示例 1:

输入: 1
输出: true
解释: $2^0$ = 1

示例 2:

输入: 16
输出: true
解释: $2^4$ = 16

示例 3:

输入: 218
输出: false

解题思路分析

方法一，mod
方法二，log => int
方法三，位运算，判断是否仅有一个 1

解法代码

Java代码

class Solution {
    public boolean isPowerOfTwo(int n) {
        return n > 0 && (n & (n-1)) == 0;
    }
}

Python代码

1
2
3

class Solution:
    def isPowerOfTwo(self, n: int) -> bool:
        return n > 0 and not (n & (n-1))

问题三比特位计数（338）

问题描述

给定一个非负整数 num 。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。

示例 1:

输入: 2
输出: [0,1,1]

示例 2:

输入: 5
输出: [0,1,1,2,1,2]

解题思路分析

解法代码

Java代码

class Solution {
    public int[] countBits(int num) {
        int[] bits = new int[num+1];
        for (int i=1; i <= num; i++) {
            bits[i] = bits[i & (i-1)] + 1;
        }
        return bits;
    }
}

Python代码

class Solution:
    def countBits(self, num: int) -> List[int]:
        bits = [0]*(num+1)
        for i in range(1,num+1):
            bits[i] = bits[i & (i-1)] + 1
        return bits

问题四 N皇后 II（52）

问题描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

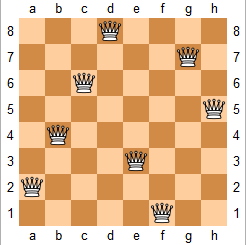
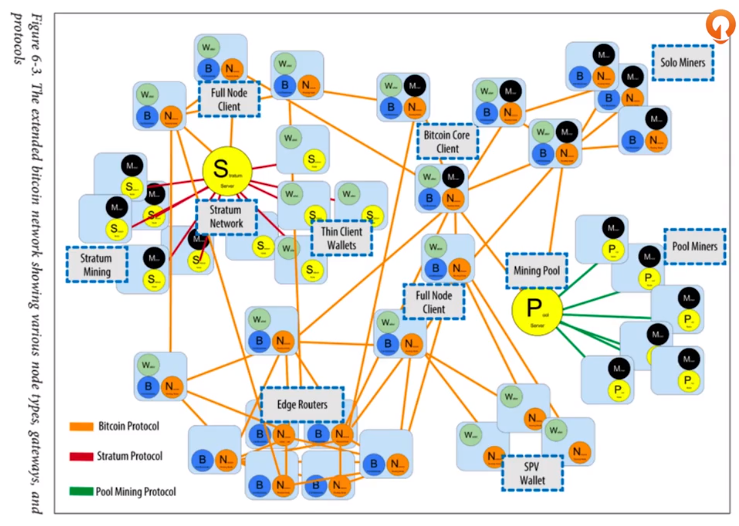
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回 n 皇后不同的解决方案的数量。

示例:

输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
[“ . Q . . “, // 解法 1
“ . . . Q “,
“ Q . . . “,
“ . . Q . “],

[“ . . Q . “, // 解法 2
“ Q . . . “,
“ . . . Q “,
“ . Q . . “]
]

解题思路分析

解法代码

Java代码

class Solution {
    int count = 0;
    public int totalNQueens(int n) {
        if (n < 1) return 0;
        DFS(n, 0, 0, 0, 0);
        return count;
    }
    public void DFS(int n, int row, int cols, int pie, int na) {
        if (row >= n) {
            count++;
            return;
        }
        int bits = (~(cols | pie | na) & ((1 << n) - 1));
        while (bits > 0) {
            int p = bits & -bits;
            DFS(n, row+1, cols | p, (pie | p) << 1, (na | p) >> 1);
            bits &= bits -1;
        }
    }
}

Python代码

class Solution:
    def totalNQueens(self, n: int) -> int:
        if n < 1: return []
        self.count = 0
        self.DFS(n, 0, 0, 0, 0)
        return self.count
    
    def DFS(self, n, row, cols, pie, na):
        # recursion terminator
        if row >= n:
            self.count += 1
            return
        # 得到当前所有的空位
        bits = (~(cols | pie | na)) & ((1 << n) - 1)
        
        while bits:
            p = bits & -bits # 得到最低位的 1
            self.DFS(n, row + 1, cols | p, (pie | p) << 1, (na | p) >> 1)
            bits = bits & (bits - 1) # 去掉最低位的 1

总结：使用位运算，代码简洁、逻辑清晰、运算快，但是理解起来有难度！

动态规划（Dynamic Programming）

递归 + 记忆化 -> 递推
状态的定义：opt[n]，dp[n]，fib[n]
状态转移方程：opt[n] = best_of(opt[n-1],opt[n-2],…)
最优子结构

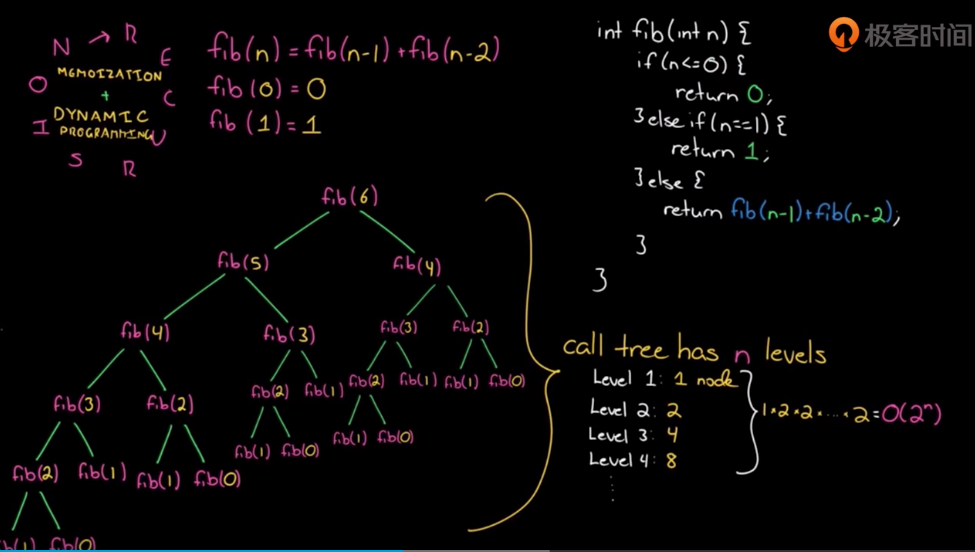
斐波那契数列

$0, 1, 1, 2, 3, 5, 8, 13, 21, …$

递推公式:$F[n] = f[n-1] + F[n-2]$

59_1_Fibonacci

59_2__Fibonacci

COUNT THE PATHS

60_1_count_the_paths

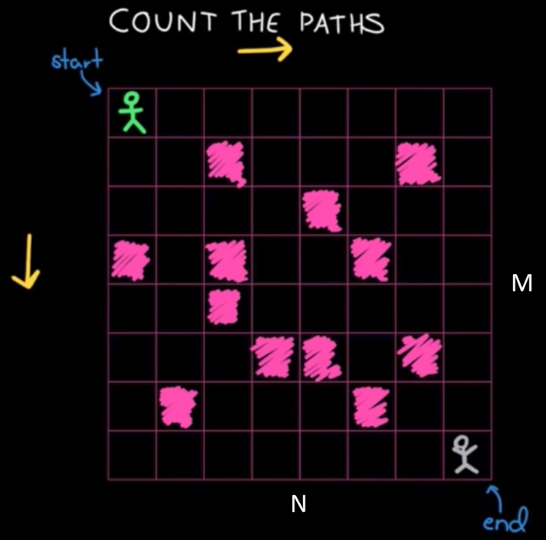
绿色小人从起点走到终点，只能向右或下方移动（不能回退），粉色格子不能进入，请问一共有多少总路线？

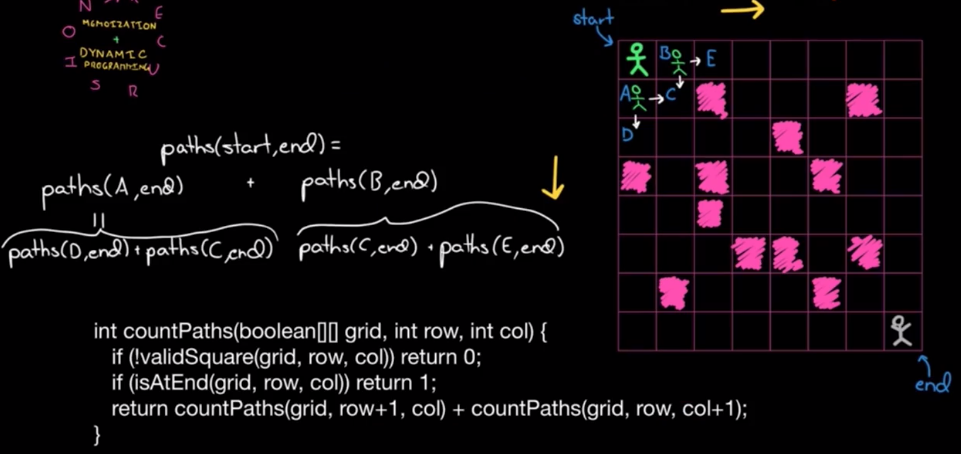
60_2_count_the_paths

动态规划的状态转移方程：
$$ opt[ i, j ] = opt[ i-1, j ] + opt[ i, j-1 ] $$

DP vs 回溯 vs 贪心

回溯（递归） —— 重复计算
贪心 —— 永远局部最优
DP —— 记录局部最优子结构 / 多种记录值

代码实战

问题一爬楼梯（70）

问题描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释：有两种方法可以爬到楼顶。

1 阶 + 1 阶

2 阶

示例 2：

输入： 3
输出： 3
解释：有三种方法可以爬到楼顶。

1 阶 + 1 阶 + 1 阶

1 阶 + 2 阶

2 阶 + 1 阶

解题思路分析

方法一，回溯递归
方法二，动态规划

解法代码

Java代码

class Solution {
    public int climbStairs(int n) {
        if (n==0 || n==1 || n==2) return n;
        int a = 1, b = 2;
        int res = 0;
        while (n != 2) {
            res = a + b;
            a = b;
            b = res;
            n -= 1;
        }
        return res;
    }
}

Python代码

class Solution:
    def climbStairs(self, n: int) -> int:
        x, y = 1, 1
        for _ in range(1, n):
            x, y = y, x + y
        return y

总结：该题的本质就是计算斐波拉契数列。

问题二三角形最小路径和（120）

问题描述

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
例如，给定三角形：

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：

如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。

解题思路分析

方法一，递归，时间复杂度 $O(2^n)$
方法二，贪心，该方法可能无法得到全局最优，不可行
方法三，动态规划，时间复杂度 $O(m \cdot n)$
①定义一个数组：$DP[i, j]$，表示从下往上走到达该点路径和的最小值。最后结果存在于$DP[0, 0]$。
②方程：$DP[i, j] = min(DP[i+1, j], DP[i+1, j+1]) + Triangle[i, j]$。
③初始值：$DP[m-1, j] = Triangle[m-1, j]$

解法代码

Java代码

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        List<Integer> mini = triangle.get(triangle.size()-1);
        for (int i = triangle.size()-2; i>=0; --i)
            for (int j = 0; j < triangle.get(i).size(); ++j)
                mini.set(j, triangle.get(i).get(j) + Math.min(mini.get(j), mini.get(j+1)));
        return mini.get(0);
    }
}

Python代码

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        res = triangle[-1]
        for i in range(len(triangle)-2, -1, -1):
            for j in range(i+1):
                res[j] = triangle[i][j] + min(res[j], res[j+1])
        return res[0]

总结：Python 在写 for 循环的时候，语法比较特别，如何需要逆序（index 从大到小）循环遍历，可以使用语句：range(n-1,-1,-1) 或者 reversed(list)。

问题三乘积最大子序列（152）

问题描述

给定一个整数数组 nums ，找出一个序列中乘积最大的连续子序列（该序列至少包含一个数）。

示例 1:

输入: [2, 3, -2, 4]
输出: 6
解释: 子数组 [2, 3] 有最大乘积 6。

示例 2:

: [-2, 0, -1]
输出: 0
解释: 结果不能为 2, 因为 [-2, -1] 不是子数组。

解题思路分析

方法一，暴力求解，使用递归
方法二，DP动态规划

解法代码

Java代码

class Solution {
    public int maxProduct(int[] nums) {
        int max = Integer.MIN_VALUE, imax = 1, imin = 1; 
        for(int i=0; i<nums.length; i++){
            if(nums[i] < 0){ int tmp = imax; imax = imin; imin = tmp;} 
            imax = Math.max(imax*nums[i], nums[i]);
            imin = Math.min(imin*nums[i], nums[i]);
            
            max = Math.max(max, imax);
        }
        return max;
    }
}

Python代码

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        if nums is None: return 0;
        
        dp = [[0 for _ in range(2)] for _ in range(2)]
        dp[0][1], dp[0][0], res = nums[0], nums[0], nums[0]
        
        for i in range(1, len(nums)):
            x, y = i % 2, (i-1) % 2
            dp[x][0] = max(dp[y][0] * nums[i], dp[y][1] * nums[i], nums[i])
            dp[x][1] = min(dp[y][0] * nums[i], dp[y][1] * nums[i], nums[i])
            res = max(res, dp[x][0])
            
        return res

问题四买卖股票的最佳时机 IV（188）

问题描述

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2:

输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

类似题型：121,122,123,309,188,714

解题思路分析

使用动态规划的算法，关键是要找到状态转移方程。
状态转移方程：
$MP[i,k,0] = max(MP[i-1,k,0], MP[i-1,k-1,1]+P[i])$
$MP[i,k,1] = max(MP[i-1,k,1], MP[i-1,k,0]-P[i])$
其中，$MP[i][k][j]$，$i$ 表示天数（取值范围【0，n-1】），$k$ 表示交易次数（取值范围【0，k】）$j$ 表示是否持有股票（0：不持有；1：持有）

解法代码

Java代码

class Solution {
    public int maxProfit(int k, int[] prices) {
        if(k < 1) return 0;
        if(k >= prices.length/2) {
            int max = 0;
            for(int i = 1; i < prices.length; ++i) {
                if(prices[i] > prices[i-1])
                    max += prices[i] - prices[i-1];
            }
            return max;
        }
        int[][] t = new int[k][2];
        for(int i = 0; i < k; ++i)
            t[i][0] = Integer.MIN_VALUE;
        for(int p : prices) {
            t[0][0] = Math.max(t[0][0], -p);
            t[0][1] = Math.max(t[0][1], t[0][0] + p);
            for(int i = 1; i < k; ++i) {
                t[i][0] = Math.max(t[i][0], t[i-1][1] - p);
                t[i][1] = Math.max(t[i][1], t[i][0] + p);
            }
        }
        return t[k-1][1];
    }
}

Java 代码解题思路与上述分析稍微有点区别，但同样也是用到了动态规划思想。t[i][0]和t[i][1]分别表示第 i 比交易买入和卖出时各自的最大收益

Python代码

class Solution:
    def maxProfit(self, k: int, prices: List[int]) -> int:
        if len(prices) < 2 or k < 1: return 0
        
        if k > len(prices) // 2 :
            res = 0
            for i in range(1, len(prices)):
                res = res + max(0, prices[i] - prices[i-1])
            return res
        
        res = 0
        mp = [[[0 for _ in range(2)] for _ in range(k+1)] for _ in range(len(prices))]
        
        for i in range(k+1):
            mp[0][i][0], mp[0][i][1] = float('-inf'), float('-inf')
                
        mp[0][0][0], mp[0][0][1] = 0, -prices[0]
                
        for i in range(1, len(prices)):
            for j in range(k+1):
                if j == 0: 
                    mp[i][j][0] = mp[i-1][j][0]
                else: 
                    mp[i][j][0] = max(mp[i-1][j][0], mp[i-1][j-1][1]+prices[i])
                mp[i][j][1] = max(mp[i-1][j][1], mp[i-1][j][0]-prices[i])
                
        end = len(prices) - 1
        for i in range(k+1):
            if mp[end][i][0] > res:
                res = mp[end][i][0]
        return res

总结：leetcode 上给出的测试用例有点变态，会把 k 值设置的很大，超过了 prices 数组本身长度，该题就变成了无限制交易次数的情况，如果不作该判断，可能会造成代码运行超时。

问题五最长上升子序列（300）

问题描述

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例:

输入: [10, 9, 2, 5, 3, 7, 101, 18]
输出: 4
解释: 最长的上升子序列是 [2, 3, 7, 101]，它的长度是 4。

说明:

可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。
你算法的时间复杂度应该为 $O(n^2)$ 。

解题思路分析

方法一，暴力求解：每个元素都有选与不选两种情况，时间复杂度 $O(2^n)$
方法二，动态规划：时间复杂度 $O(n^2)$
① 定义状态：$DP[i]$，表示从头 → $i$ 元素（$i$ 必选）的最长子序列的长度
② 状态转移方程：
$$DP[i] = max{DP[j]} + 1,j < i,nums[i] > nums[j]$$
③ 结果为 $max{DP[0],DP[1],DP[2],\cdots,DP[n-1]}$
方法三，二分查找：通过二分查找，优化一个最长上升子序列 LIS，时间复杂度 $O(nlogn)$ 。元素插入规则：若新进元素大于 LIS 中最后一个元素，直接放到 LIS 最后，否则找到比其大的所有元素的最小者，进行替换。

解法一：动态规划

Java代码

class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums == null || nums.length ==0)
            return 0;
        int res = 1;
        int[] dp = new int[nums.length];
        for (int i=0; i < nums.length; i++) 
            dp[i] = 1;
        
        for (int i=1; i < nums.length; i++) {
            for (int j=0; j < i; j++) {
                if (nums[j] < nums[i])
                    dp[i] = Math.max(dp[i], dp[j]+1);
            }
            res = Math.max(dp[i], res);
        }
        return res;
    }
}

Python代码

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums: return 0
        
        dp = [1 for _ in range(len(nums))]
        n = len(nums)
        for i in range(1, n):
            for j in range(0, i):
                if nums[j] < nums[i]:
                    dp[i] = max(dp[i], dp[j]+1)
            
        res = 1;
        for i in range(0, n):
            if dp[i] > res:
                res = dp[i]
        
        return res

解法二：二分查找

Java代码

class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums == null || nums.length == 0)
            return 0;
        List<Integer> list = new ArrayList<>();
        for (int item: nums) {
            if (list.size() == 0 || item > list.get(list.size()-1))
                list.add(item);
            else {
                int index = find(list, item);
                list.set(index, item);
            }       
        }
        return list.size();
    }
    public int find(List<Integer> list, int val) {
        int low = 0;
        int high = list.size()-1;
        while (low <= high) {
            int mid = (low + high) / 2;
            if (list.get(mid) < val)
                low = mid + 1;
            else if (list.get(mid) > val)
                high = mid - 1;
            else return mid;
        }
        return low;
    }
}

Python代码

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums: return 0
        
        lis = []
        for item in nums:
            if lis == [] or item > lis[-1]:
                lis.append(item)
            else:
                index = self.find(lis, item)
                lis[index] = item
        
        return len(lis)
    
    def find(self, lis: List[int], val: int) -> int:
        low, high = 0, len(lis)-1
        
        while low <= high:
            mid = (low + high) // 2
            if lis[mid] < val:
                low = mid + 1
            elif lis[mid] > val:
                high = mid - 1
            else:
                return mid
        return low

总结：该解题思路比较巧妙，按照正常的思维很难想得到，但是时间复杂度是最低的，也是最高效的方法。

问题六零钱兑换（322）

问题描述

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:

输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1

示例 2:

输入: coins = [2], amount = 3
输出: -1

说明:

你可以认为每种硬币的数量是无限的。

解题思路分析

该问题可以转化为一个爬楼梯的问题：硬币为每次所走的楼梯数，总金额为所要到达的楼层数。

方法一，暴力求解：计算每个硬币的取值范围，枚举所有情况。
方法二，动态规划
① 定义状态：DP[i]，表示上到第 i 阶台阶最小的步数
② 状态转移方程：
$$DP[i] = min{DP[i-coins[j]]} + 1$$
③ 结果为 $DP[amount]$

解法代码

Java代码

class Solution {
    public int coinChange(int[] coins, int amount) {
        int Max = amount + 1;
        int[] dp = new int[amount+1];
        Arrays.fill(dp, Max);
        dp[0] = 0;
        for (int i=1; i <= amount; i++) {
            for (int j=0; j < coins.length; j++) {
                if (coins[j] <= i)
                    dp[i] = Math.min(dp[i-coins[j]]+1, dp[i]);
            }
        }
        return dp[amount] == Max ? -1:dp[amount];
    }
}

Python代码

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [amount+1] * (amount+1)
        dp[0] = 0
        for i in range(amount+1):
            for j in range(len(coins)):
                if coins[j] <= i:
                    dp[i] = min(dp[i-coins[j]]+1, dp[i])
        if dp[amount] == amount+1: return -1
        else: return dp[amount]

问题七编辑距离（72）

问题描述

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1:

输入: word1 = “horse”, word2 = “ros”
输出: 3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)

示例 2:

输入: word1 = “intention”, word2 = “execution”
输出: 5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

解题思路分析

使用动态规划方法：
① 定义状态：$DP[i,j]$，表示 word1 的前 i 个字符变换到 word2 的前 j 个字符最少步数。
② 状态转移方程：
$$DP[i,j]=\left{\begin{array}{llll}{DP[i-1,j-1]} &,& word1[i]=word1[j] \\ {1+min(DP[i-1,j],DP[i,j-1],DP[i-1,j-1])} &,& otherwise \end{array}\right.$$
③ 结果为 $DP[m, n]$，m 为 word1 的长度，n 为 word2 的长度。

解法代码

Java代码

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();
        int[][] dp = new int[m+1][n+1];
        int max = 0;
        for (int i=0; i<=m; i++) dp[i][0] = i;
        for (int j=0; j<=n; j++) dp[0][j] = j;
        
        for (int i=1; i<=m; i++) {
            for (int j=1; j<=n; j++) {
                if (word1.charAt(i-1) == word2.charAt(j-1))
                    dp[i][j] = dp[i-1][j-1];
                else
                    dp[i][j] = 1+((max=(dp[i-1][j]<dp[i][j-1])?dp[i-1][j]:dp[i][j-1])<dp[i-1][j-1]?max:dp[i-1][j-1]);
            }
        }
        return dp[m][n];
    }
}

Python代码

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        m, n = len(word1), len(word2)
        dp = [[0 for _ in range(n+1)] for _ in range(m+1)]
        
        for i in range(m+1): dp[i][0] = i
        for j in range(n+1): dp[0][j] = j
            
        for i in range(1, m+1):
            for j in range(1, n+1):
                if word1[i-1]==word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])
                
        return dp[m][n]

总结：该题是一个比较经典的面试题，需要好好理解其动态规划思想。其中 Java 的代码中有一个获取三个值中最小值的语法 int min = ((min=(a<b)?a:b)<c?min:c); 需要特别留意。

并查集（union & find）

并查集(union & find) 是一种树型的数据结构，用于处理一些不交集(Disjoint Sets)的合并及查询问题。
Find: 确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
Union: 将两个子集合并成同一个集合。

在生活中的例子

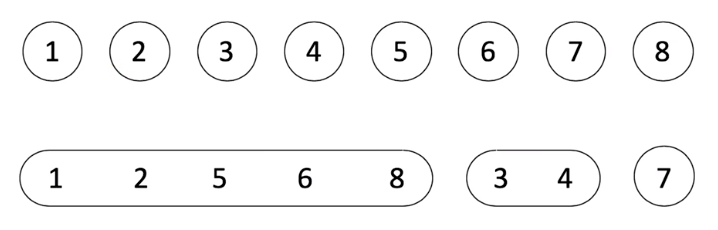
62_union_find

小弟 -> 老大
帮派识别
两种优化方式

并查集代码实现

63_code

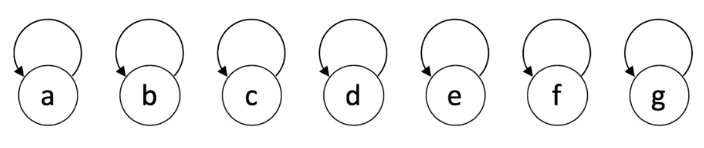
64_1_structure

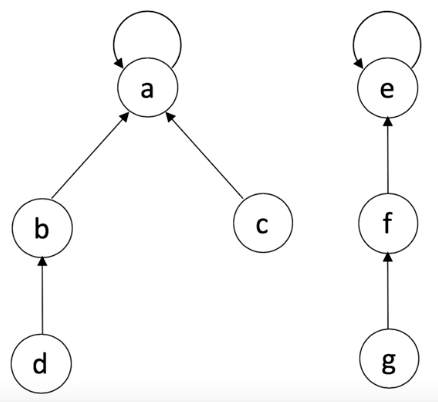
64_2_structure

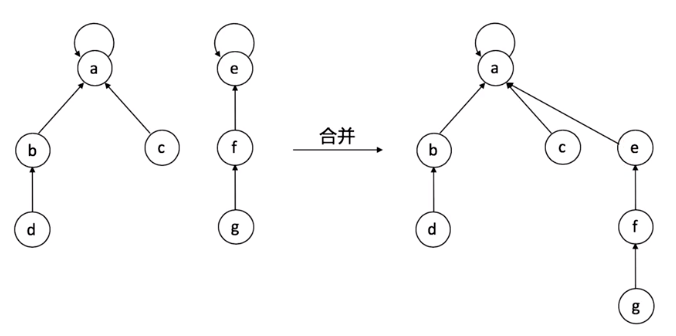
64_3_structure

并查集优化

优化一

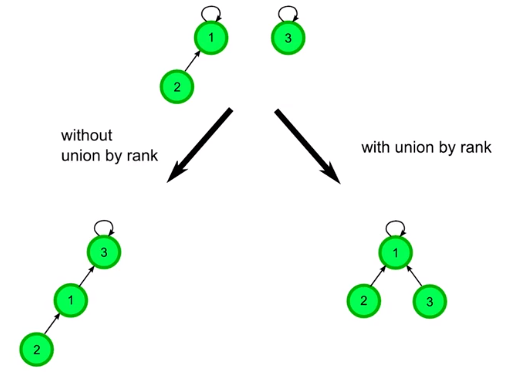
65_optimize1

优化代码：
66_optimize_code

优化二

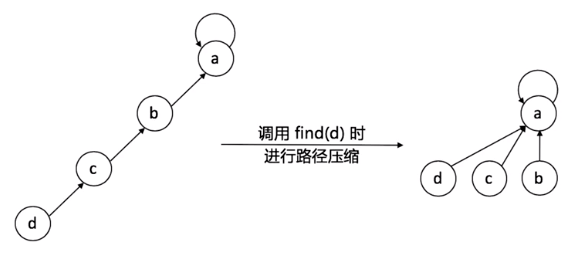
67_optimize2

代码实战

问题一岛屿的个数（200）

问题描述

给定一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。

示例 1:

输入:
11110
11010
11000
00000
输出: 1

示例 2:

输入:
11000
11000
00100
00011
输出: 3

解题思路分析

方法一，染色问题：遍历所有节点，若节点等于 1，count++，将该节点所有相邻节点以及相邻节点的相邻节点变为 0（DFS 或 BFS），不断循环直到所有节点变为 0，最后返回 count 。
方法二，并查集
① 初始化：针对 1 节点指向自身；
② 遍历所有节点，相邻 1 节点合并，0 节点不管；
③ 遍历 parents

解法代码

Java代码

1
2

Python代码

1
2

问题二朋友圈（547）

问题描述

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果 M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

示例 1:

输入:
[[1,1,0],
[1,1,0],
[0,0,1]]
输出: 2
说明：已知学生0和学生1互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。

示例 2:

输入:
[[1,1,0],
[1,1,1],
[0,1,1]]
输出: 1
说明：已知学生 0 和学生 1 互为朋友，学生 1 和学生 2 互为朋友，所以学生 0 和学生 2 也是朋友，所以他们三个在一个朋友圈，返回 1。

注意：

N 在 [1,200] 的范围内。
对于所有学生，有 M[i][i] = 1 。
如果有 M[i][j] = 1，则有 M[j][i] = 1。

解题思路分析

该题可以直接转化为 问题一岛屿问题，解题代码一样。

解法代码

略

LRU Cache

记忆
钱包 - 储物柜
代码模板

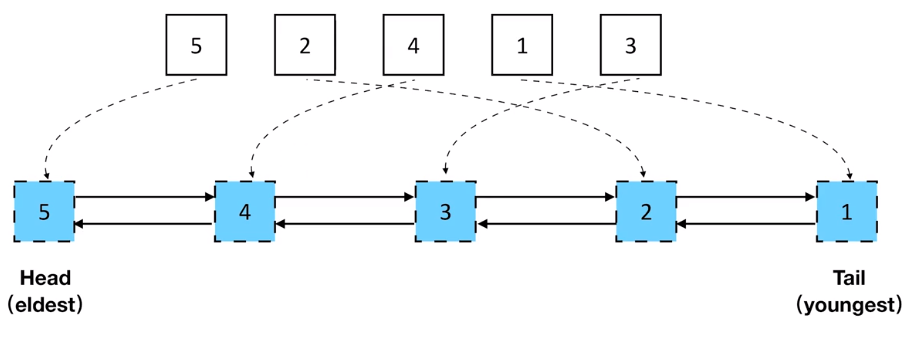
LRU Cache 特点

68_cache

Least recently used
Double LinkedList
$O(1)$查询
$O(1)$修改、更新

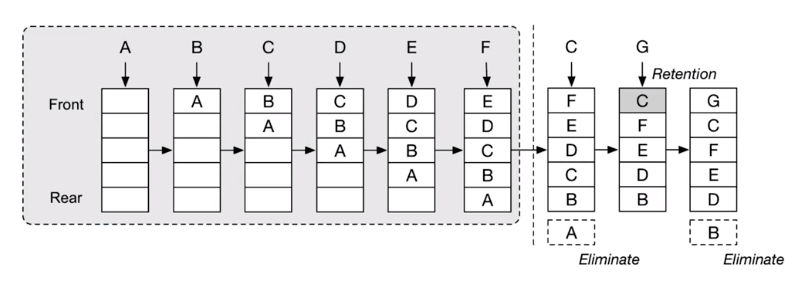
替换算法原理

69_LRU

70_Double_Link

LFU Cache

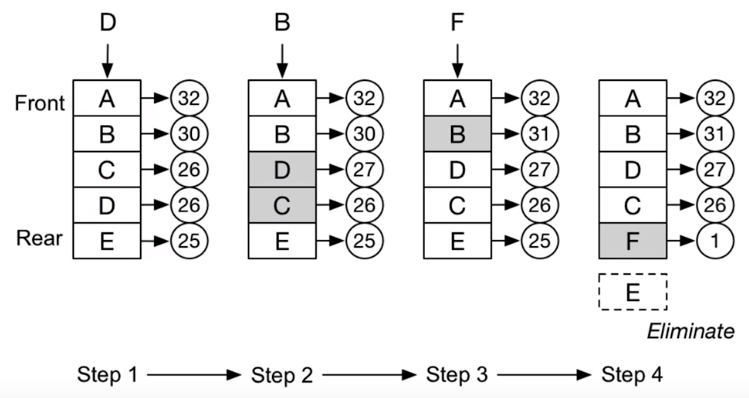
LFU - least frequently used
最近最不常用页面替换算法
LRU - least recently used
最近最少使用页面替换算法

71_LFU

代码实战

问题一 LRU缓存机制（146）

问题描述

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作：获取数据 get 和写入数据 put 。

获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。
写入数据 put(key, value) - 如果密钥不存在，则写入其数据值。当缓存容量达到上限时，它应该在写入新数据之前删除最近最少使用的数据值，从而为新的数据值留出空间。

进阶:
你是否可以在 $O(1)$ 时间复杂度内完成这两种操作？

示例:

LRUCache cache = new LRUCache( 2 // 缓存容量 // );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // 返回 1
cache.put(3, 3); // 该操作会使得密钥 2 作废
cache.get(2); // 返回 -1 (未找到)
cache.put(4, 4); // 该操作会使得密钥 1 作废
cache.get(1); // 返回 -1 (未找到)
cache.get(3); // 返回 3
cache.get(4); // 返回 4

解题思路分析

解法代码

Java代码

class LRUCache {
    LinkedHashMap<Integer, Integer> map = null;
    public LRUCache(int capacity) {
        this.map = new LinkedHashMap(capacity) {
            protected boolean removeEldestEntry(Map.Entry eldest) {
            return size() > capacity;
            }
        };
    }
    
    public int get(int key) {
        if (map.containsKey(key)) {
            int v = map.remove(key);
            map.put(key, v);
            return v;
        }
        else return -1;
    }
    
    public void put(int key, int value) {
        if (map.containsKey(key)) {
            map.remove(key);
            map.put(key, value);
        }
        else {
            map.put(key, value);
        }    
    }
}

Python代码

class LRUCache:

    def __init__(self, capacity: int):
        self.queue = collections.OrderedDict()
        self.remain = capacity

    def get(self, key: int) -> int:
        if key not in self.queue:
            return -1
        else:
            v = self.queue.pop(key)
            self.queue[key] = v
            return v

    def put(self, key: int, value: int) -> None:
        if key in self.queue:
            self.queue.pop(key)
        else:
            if self.remain == 0:
                self.queue.popitem(last=False)
            else:
                self.remain -= 1
        self.queue[key] = value

总结：Java 代码最关键的部分为在初始化 LinkedHashMap 实例的同时重载了 removeEldestEntry 方法，该方法的重载使得当实例调用 put 方法时，如果缓存达到最大值 capacity，则自动移除最先插入缓存的元素。而 Python 的代码需要自己手动判断缓存是否达到最大值。

Bloom Filter（布隆过滤器）

哈希函数回顾

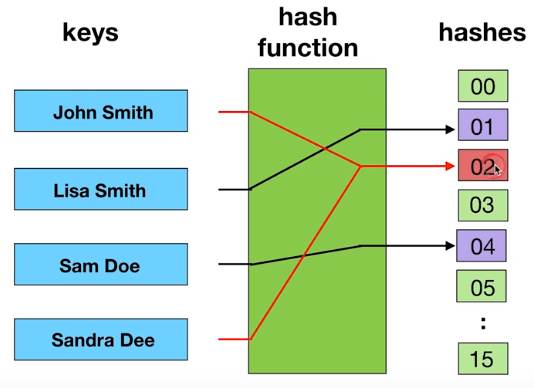
72_hash

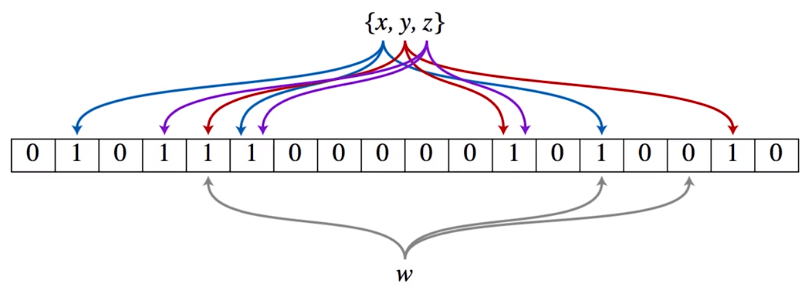
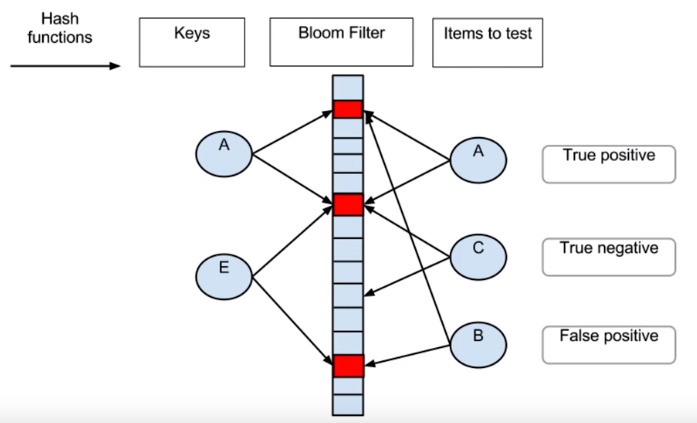
布隆过滤器的特点

一个很长的二进制向量和一个映射函数。

布隆过滤器可以用于检索一个元素是否在一个集合中。

它的优点是空间效率和查询时间都远远超过一般的算法，缺点是有一定的误识别率（仅针对判断元素是否存在于集合而言，对于判断是否不存在是100%正确的）和删除困难。

73_Bloom

74_Bloom

案列

比特币
Redis VS BloomFilter
分布式系统（Map-Reduce）

比特币网络

75_1_bitscoins

75_2_bitscoins

位运算

什么是位运算

常见的位运算符

XOR - 异或

代码实战

问题一 位1的个数（191）

问题描述

解题思路分析

解法代码

问题二 2的幂（231）

问题描述

解题思路分析

解法代码

问题三 比特位计数（338）

问题描述

解题思路分析

解法代码

问题四 N皇后 II（52）

问题描述

解题思路分析

解法代码

动态规划（Dynamic Programming）

斐波那契数列

COUNT THE PATHS

DP vs 回溯 vs 贪心

代码实战

问题一 爬楼梯（70）

问题描述

解题思路分析

解法代码

问题二 三角形最小路径和（120）

问题描述

解题思路分析

解法代码

问题三 乘积最大子序列（152）

问题描述

解题思路分析

解法代码

问题四 买卖股票的最佳时机 IV（188）

问题描述

解题思路分析

解法代码

问题五 最长上升子序列（300）

问题描述

解题思路分析

解法一：动态规划

解法二：二分查找

问题六 零钱兑换（322）

问题描述

解题思路分析

解法代码

问题七 编辑距离（72）

问题描述

解题思路分析

解法代码

并查集（union & find）

在生活中的例子

并查集代码实现

并查集优化

优化一

优化二

代码实战

问题一 岛屿的个数（200）

问题描述

解题思路分析

解法代码

问题二 朋友圈（547）

问题描述

解题思路分析

解法代码

LRU Cache

LRU Cache 特点

替换算法原理

LFU Cache

代码实战

问题一 LRU缓存机制（146）

问题描述

解题思路分析

解法代码

Bloom Filter（布隆过滤器）

问题一位1的个数（191）

问题三比特位计数（338）

问题一爬楼梯（70）

问题二三角形最小路径和（120）

问题三乘积最大子序列（152）

问题四买卖股票的最佳时机 IV（188）

问题五最长上升子序列（300）

问题六零钱兑换（322）

问题七编辑距离（72）

问题一岛屿的个数（200）

问题二朋友圈（547）