数据结构与算法笔记 (二)

递归 & 分治

Recursion
Divide & Conquer

Recursion 递归 — 循环

递归就是通过函数体来进⾏的循环！

举个栗子：
计算 $n!$，计算公式：$ n! = 1 \cdot 2 \cdot 3 \cdot … \cdot n $

def Fatorial(n):
    if n <= 1:
        return 1
    return n * Factorial(n - 1)

递归过程如下图：

举个栗子：
计算斐波拉契数列 Fibonacci array: $1, 1, 2, 3, 5, 13, 21, 34, …$
计算公式：$F(n) = F(n-1) + F(n-2)$

def fib(n):
    if n == 0 or n == 1:
        return n
    return fib(n-1) + fib(n-2)

下图为 F(6) 的计算过程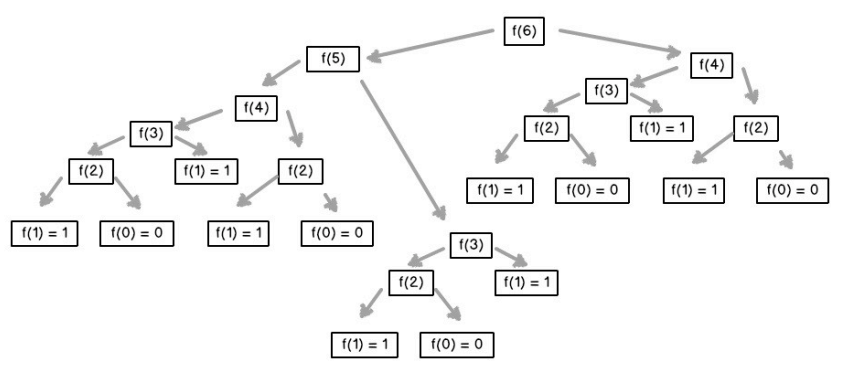

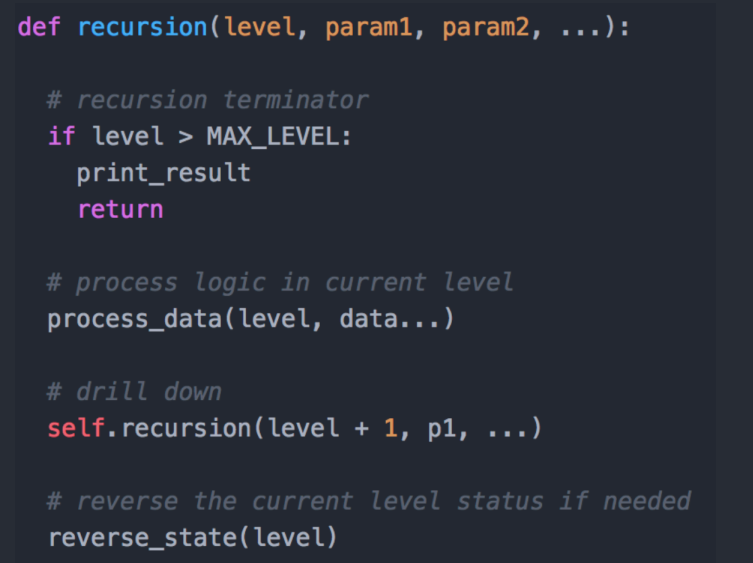
递归代码通用模板

分治 - Divde & Conquer

算法逻辑图：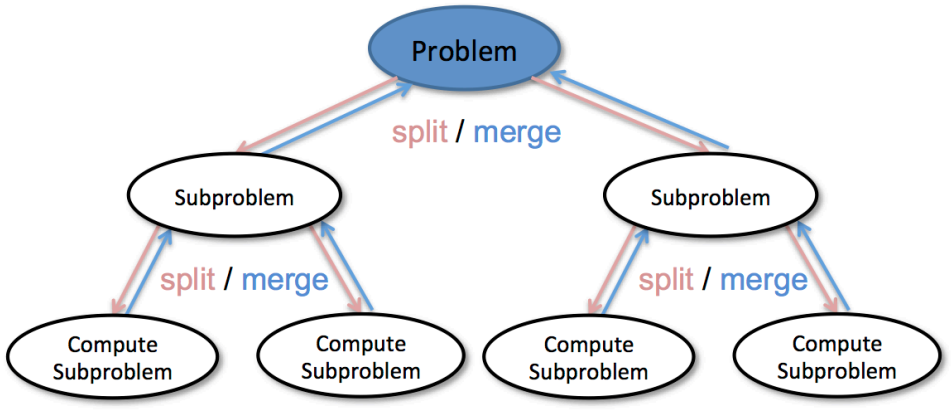

举个列子，将链表中的元素变成大写

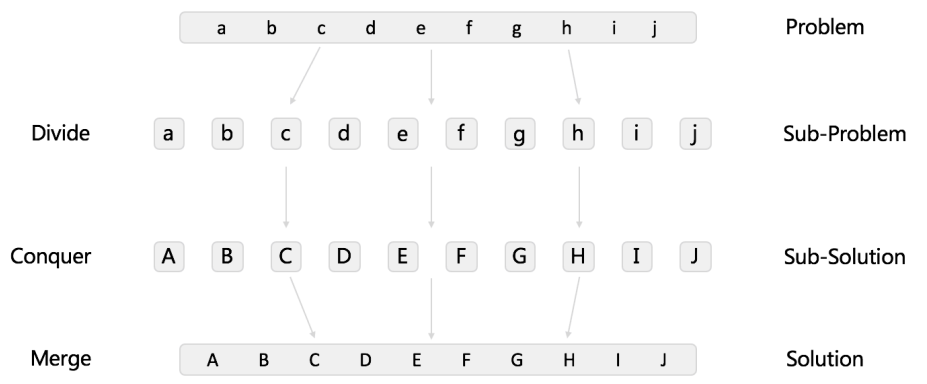
咋看之下，使用分治与循环并无区别，但是分治算法每一个子问题互不相关，所以可以使用并行计算的方式加速。

分治代码通用模板

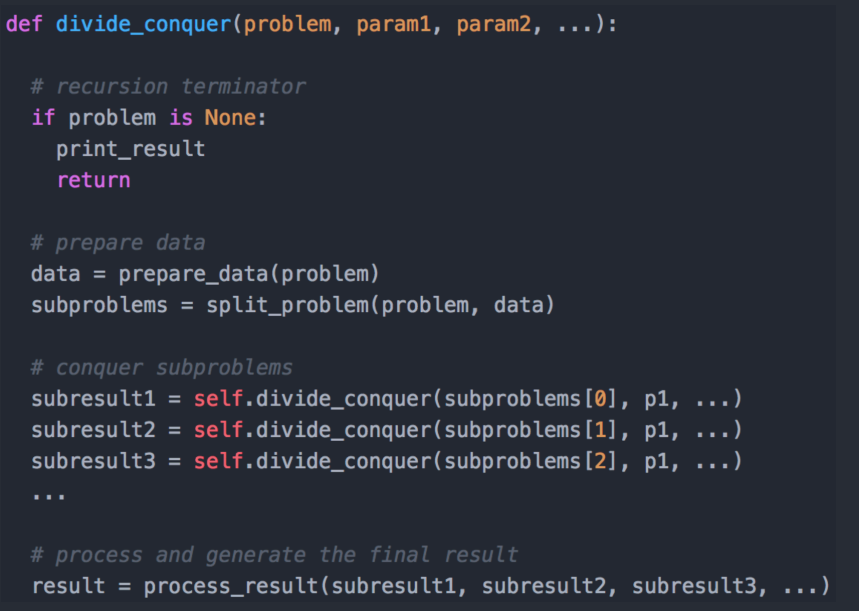
代码实战

问题一 Pow(x, n)（50）

问题描述

实现 pow(x, n) ，即计算 x 的 n 次幂函数

示例 1:

输入: 2.00000, 10
输出: 1024.00000

示例 2:

输入: 2.10000, 3
输出: 9.26100

示例 3:

输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25

说明:

-100.0 < x < 100.0
n 是 32 位有符号整数，其数值范围是 [−231, 231 − 1] 。

解题思路分析

方法一，调用库函数，时间复杂度 $O(1)$
方法二，暴力循环，时间复杂度 $O(n)$
方法三，分治：
① $target = x^n$；
② 当 $n$ 为偶数，分两段子问题，$y = x ^{n/2}$，$result = y^2$；
③ 当 $n$ 为奇数，也分两段子问题，$y = x ^{(n-1)/2}$，$result = xy^2$；
④ 终止条件，$x^1$ or $x^0$

解法代码

Java代码

class Solution {
    public double myPow(double x, int n) {
        double res = 1.0;
        for(int i=n; i != 0; i /= 2){
            if(i%2 != 0){
                res *= x;
            }
            x *= x;
        }
        return n < 0 ? 1/res : res;
    }
}

Python代码

class Solution:
    def myPow(self, x: float, n: int) -> float:
        if n == 0: return 1
        elif n == 1: return x
        elif n < 0: return 1 / self.myPow(x, -n)
        if n % 2 == 0:
            return self.myPow(x*x, n/2)
        else:
            return x*self.myPow(x*x, n//2)

class Solution:
    def myPow(self, x: float, n: int) -> float:
        if n < 0:
            x = 1/x
            n = -n
        pow = 1
        while n:
            if n & 1:
                pow*= x
            x *= x
            n >>= 1
        return pow

总结：python 的第二段代码为最佳代码实现，利用位运算符的特性求解。Java 也是分治的思想，只不过利用循环实现的机制比较巧妙。

问题二求众数（169）

问题描述

给定一个大小为 n 的数组，找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在众数。

示例 1:

输入: [3,2,3]
输出: 3

示例 2:

输入: [2,2,1,1,1,2,2]
输出: 2

解题思路分析

方法一，暴力求解：写两层嵌套循环，第一层循环枚举所有元素，第二层循环计算该元素出现的次数，时间复杂度 $O(N^2)$ 。
方法二，利用 Map：一次循环计算出所有元素出现次数，时间复杂度 $O(N)$，空间复杂度 $O(N)$ 。
方法三，排序：计算重复次数，只要重复次数大于 n/2 即为所求。
方法四：分治：数组一分为二，分别放入函数求解众数，令左边结果为 left 右边结果为 right，若 left == right 说明已经找到；若不等，返回 left 和 right 出现次数较大者。

解法代码

Java代码

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        int a = 0, count = 0;
        for(int i=0; i<nums.length; i++){
            if(i == 0){
                a = nums[i];
                count++;
            }
            else {
                if(nums[i] == a)
                    count++;
                else{
                    a = nums[i];
                    count=1;
                }
            }
            if(count > nums.length/2)
                return a;
        }
        return Integer.MAX_VALUE;
    }
}

Python代码

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        dic = {}
        for item in nums:
            dic[item] = dic.get(item, 0)+1
        return max(dic, key=dic.get)

总结： Java 代码使用方法三，先对数组进行排序，然后按照顺序遍历所有元素，直到计算出出现频率 count 大于 n/2 的元素，返回该元素。 Python 的代码利用了字典，即 Map 结构，写起来比较简洁。后来悲剧的发现 Java 的代码其实只用两行就能实现，因为题目说了一定存在众数，所以排完序之后直接 return nums[nums.length/2] 。

贪⼼算法（Greedy Algorithms)

什么是贪⼼算法
何种情况下⽤到贪⼼算法

概念

贪⼼法，⼜称贪⼼算法、贪婪算法：在对问题求解时，总是做出在当前看来是最好的选择。

我们用下面的例子来理解下什么是贪心算法：

如上图所示，题目要求用 20，10，5，1 元的面值的钱币凑出恰好等于 36 元的数额，最少需要多少张纸币。贪心算法就是由大面值到小面值匹配，直至得到最优解。

但是贪心算法不一定能够得到最优解，以上题为例。如将题目改为用 10，9，1 元的面值凑出 18，如果使用贪心算法先用 10 元面值匹配，余 8，剩下 8 只能用 1 元面值匹配，贪心算法的结果就是 1 张 10 元和 8 张 1 元，这显然不是正确答案（两张 9 元）。

为何前一种情况可以使用贪心算法求解？主要系因为前一种情况的面值刚好成倍数关系。

适⽤ Greedy 的场景

简单地说，问题能够分解成⼦问题来解决，⼦问题的最优解能递推到最终问题的最优解。这种⼦问题最优解成为最优⼦结构。

贪⼼算法与动态规划的不同在于它对每个⼦问题的解决⽅案都做出选择，不能回退。动态规划则会保存以前的运算结果，并根据以前的结果对当前进⾏选择，有回退功能。

代码实战

问题一买卖股票的最佳时机 II（122）

问题描述

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

解题思路分析

方法一，DFS（深度优先搜索）：依次遍历数组，每一天都可以选择买入或者卖出，计算所有可能的结果，得出最大的盈利。时间复杂度 $O(2^n)$ 。
方法二，贪心算法：只要后一天的价格比前一天价格高，就在前一天买入后一天卖出。时间复杂度 $O(n)$ 。
方法三，动态规划 DP：后面例题讲解。时间复杂度也为 $O(n)$ 。

解法代码

Java代码

class Solution {
    public int maxProfit(int[] prices) {
        int res = 0;
        for (int i=1; i<prices.length; i++) {
            if (prices[i]>prices[i-1])
                res += prices[i]-prices[i-1];
        }
        return res;
    }
}

Python代码

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        if length<2: return 0
        dp = [[0 for _ in range(2)] for _ in range(length)]
        dp[0][0] = 0
        dp[0][1] = -prices[0]
        for i in range(1, length):
            dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
            dp[i][1] = max(dp[i-1][0]-prices[i], dp[i-1][1])
        return dp[length-1][0]

总结：Java 代码使用了贪心算法思想（解法二），Python 代码使用了动态规划的思想（解法三）。

⼴度优先搜索(BFS) 与深度优先搜索(DFS)

⼴度优先搜索(Breadth-First-Search)

在树（图/状态集）中寻找特定节点

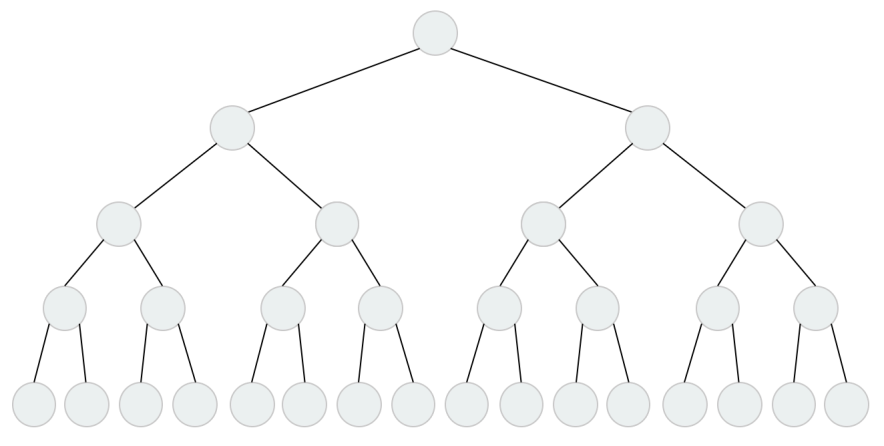
BFS 如何工作

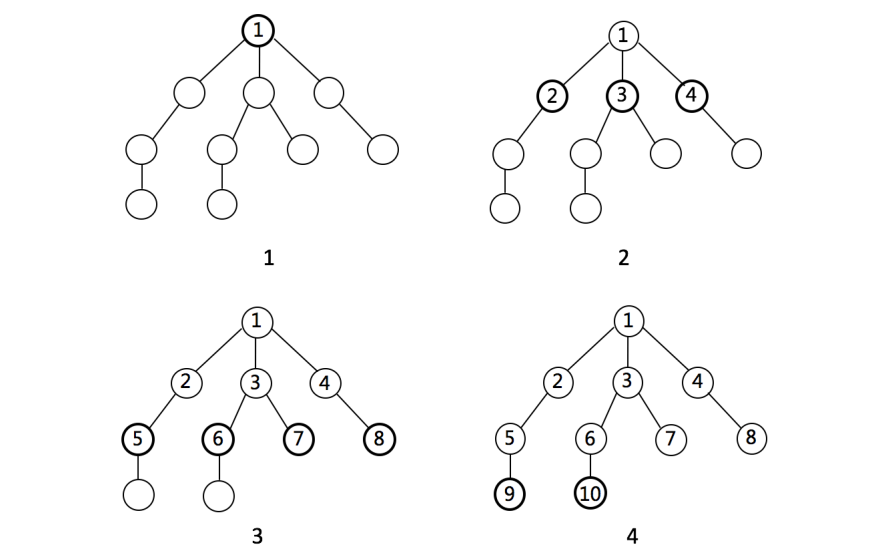
BFS 代码

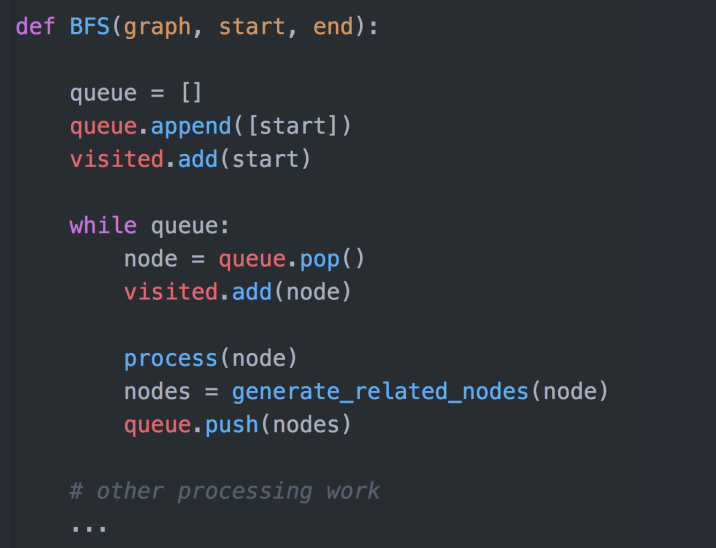
上述代码既适合于树，也适合于图。

深度优先搜索(Depth-First-Search)

DFS 如何工作

搜索树结构如下图：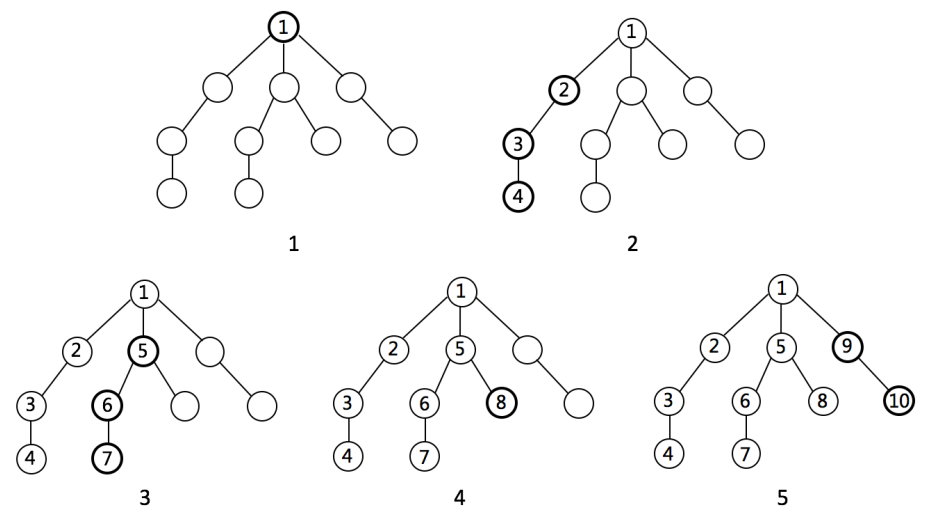

搜索图结构如下图：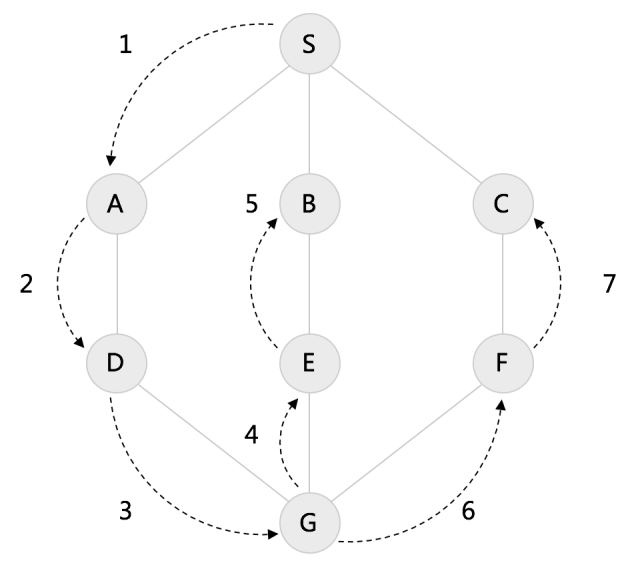

DFS 与 BFS 对比，如下图所示：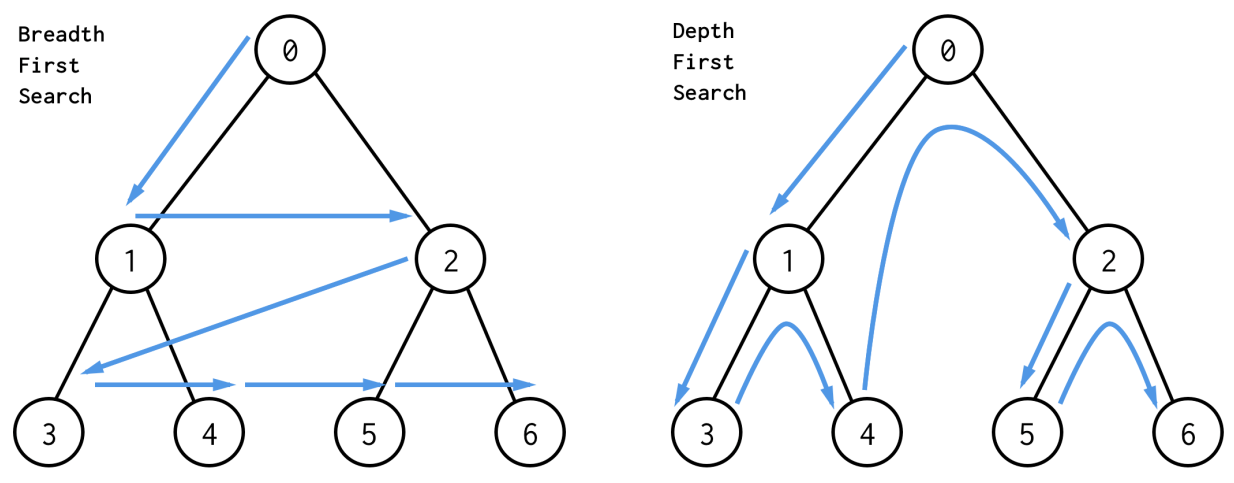

DFS 代码

递归写法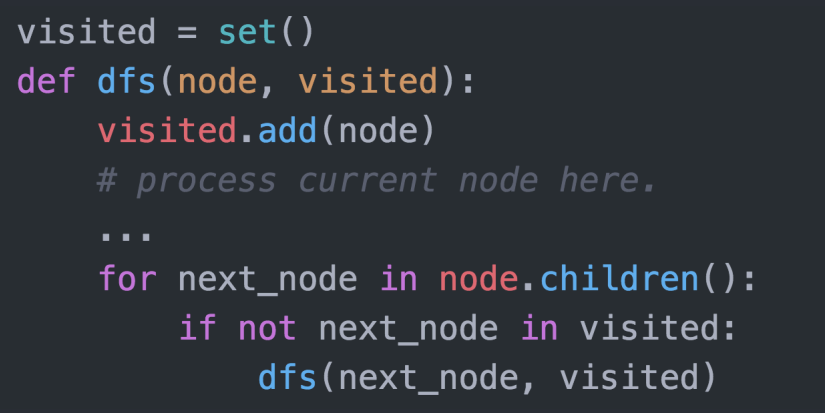

非递归写法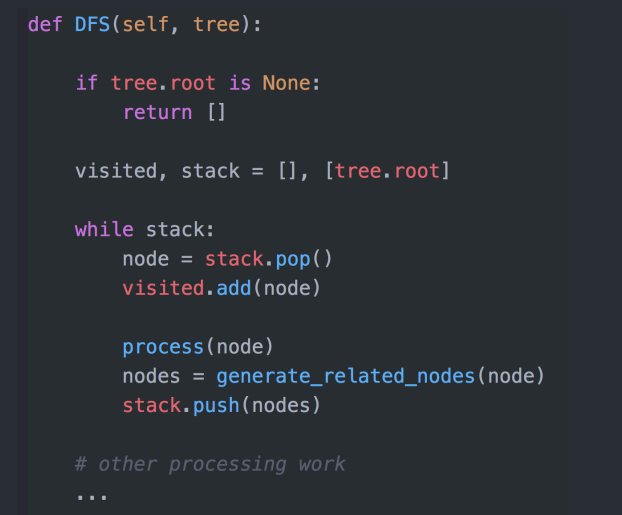

代码实战

问题一二叉树的层次遍历（102）

问题描述

给定一个二叉树，返回其按层次遍历的节点值。（即逐层地，从左到右访问所有节点）。

例如:

给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7

返回其层次遍历结果：

[
[3],
[9, 20],
[15, 7]
]

解题思路分析

方法一，BFS：① 在队列中加入层级标识符；② 写一个 for 循环，逐层扫描
方法二，DFS：建立好结果的二维数组，在遍历的同时需要记录 level ，即层级，一边遍历一边写入结果。

解法代码

Java代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null) return res;
        
        Queue<TreeNode> q = new LinkedList<>();
        q.add(root);
        
        while(!q.isEmpty()){
            int levelSize = q.size();
            List<Integer> currLevel = new ArrayList<>();
            for(int i=0; i < levelSize; i++){
                TreeNode currNode = q.poll();
                currLevel.add(currNode.val);
                if(currNode.left != null)
                    q.add(currNode.left);
                if(currNode.right != null)
                    q.add(currNode.right);
            }
            res.add(currLevel);
        }
        return res;
    }
}

Python代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root: return []
        
        result = []
        queue = collections.deque()
        queue.append(root)
        
        # visited = set(root)
        
        while queue:
            level_size = len(queue)
            current_level = []
            for _ in range(level_size):
                node = queue.popleft()
                current_level.append(node.val)
                if node.left: queue.append(node.left)
                if node.right: queue.append(node.right)
                    
            result.append(current_level)
            
        return result

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root: return []
        self.result = []
        self._dfs(root, 0)
        return self.result
        
    def _dfs(self, node, level):
        if not node: return 
        if len(self.result) < level+1:
            self.result.append([])
        self.result[level].append(node.val)
        
        self._dfs(node.left, level + 1)
        self._dfs(node.right, level + 1)

总结：Python 的第一段代码中使用了 collections 库中写好的双端队列，执行起来要比使用原生态的 [] 构造的 queue 快一倍。第二段代码使用 DFS 方法，思路比较非正常性，了解即可。

问题二二叉树的最大深度（104）

问题描述

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：

给定二叉树 [3, 9, 20, null, null, 15, 7]，

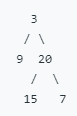
返回它的最大深度 3 。

解题思路分析

方法一，Recursion
方法二，BFS
方法三，DFS

解法一：Recursion

Java代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        return root == null ? 0
            : 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
    }
}

Python代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root: return 0;
        return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

总结：递归的代码思路比较清晰，写起来也比较简洁！

解法二：BFS or DFS

Java代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        Stack<TreeNode> stack = new Stack<>();
        Map<TreeNode, Integer> map = new HashMap<>();
        map.put(root, 1);
        stack.push(root);
        int depth = 0;
        while(!stack.isEmpty()){
            TreeNode currNode = stack.pop();
            int currDepth = map.get(currNode);
            depth = Math.max(depth, currDepth);
            if(currNode.left != null){
                stack.push(currNode.left);
                map.put(currNode.left, currDepth+1);
            }
            if(currNode.right != null){
                stack.push(currNode.right);
                map.put(currNode.right, currDepth+1);
            }
        }
        return depth;
    }
}

Python代码

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root: return 0;
        
        depth = 0;
        queue = collections.deque()
        queue.append((1, root))
        
        while queue:
            level, node = queue.popleft()
            if depth < level: depth = level
            if node.left: queue.append((level+1, node.left))
            if node.right: queue.append((level+1, node.right))
        return depth

总结： Java 的代码利用 Stack 实现 DFS,实现 DFS 搜索的过程中，利用了一个 Map 结构记录当前节点的层级；Python 的代码利用 Queue 实现 BFS 。

问题三二叉树的最小深度（111）

问题描述

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3, 9, 20, null, null, 15, 7],

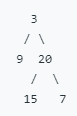
返回它的最小深度 2.

解题思路分析

同 问题二，思路与求解最大深度一样。这里进使用递归方法求解。

解法代码

Java代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int minDepth(TreeNode root) {
        if(root == null) return 0;
        if(root.left == null) return 1 + minDepth(root.right);
        if(root.right == null) return 1 + minDepth(root.left);
        return 1 + Math.min(minDepth(root.left), minDepth(root.right));
    }
}

Python代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root: return 0;
        if not root.left: return 1 + self.minDepth(root.right);
        if not root.right: return 1 + self.minDepth(root.left);
        return 1 + min(self.minDepth(root.left), self.minDepth(root.right))

总结：求解最小深度与求解最大深度的代码有点区别，在于递归的返回必须要求当前节点的左右子树均不为空，否则可能会出现问题。

问题四括号生成（22）

问题描述

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[
“ ( ( ( ) ) ) “,
“ ( ( ) ( ) ) “,
“ ( ( ) ) ( ) “,
“ ( ) ( ( ) ) “,
“ ( ) ( ) ( ) “
]

解题思路分析

方法一，数学归纳法
方法二，递归 Recursion：
① 枚举所有可能情况，在判断所有情况的合法性；$O(2^{2n})$
② 改进，1. 局部不合法，不再递归；2. 左括号和右括号都只有 n 个限制，$O(2^n)$

解法代码

Java代码

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> result = new ArrayList<>();
        gen("", result, n, n);
        return result;
    }


    public void gen(String sublist, List<String> result, int left, int right) {
        if (left == 0 && right == 0) {
            result.add(sublist);
            return;
        }
        if (left > 0) 
            gen(sublist + "(", result, left - 1, right);
        if (left < right)
            gen(sublist + ")", result, left, right - 1);
    }
}

Python代码

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        self.list = []
        self._gen(0, 0, n, "")
        return self.list
    
    def _gen(self, left, right, n, result):
        if left == n and right == n:
            return self.list.append(result)
        if left < n:
            self._gen(left + 1, right, n, result + "(")
        if left > right and right < n:
            self._gen(left, right + 1, n, result + ")")

总结： Java 代码中 left 和 right 指代剩余括号数量，Python 代码中 left 和 right 指代已使用括号数量。

剪枝

剪枝图例

九宫格状态空间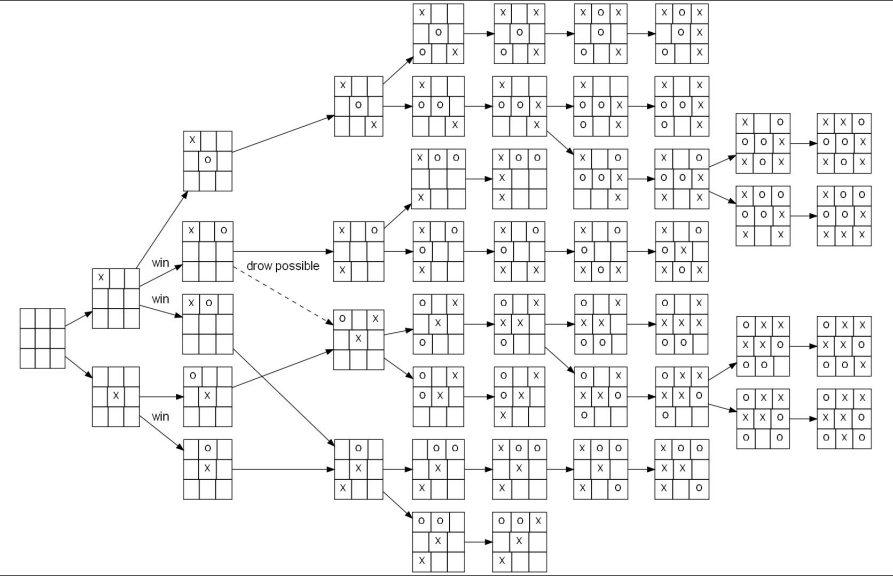

其他棋类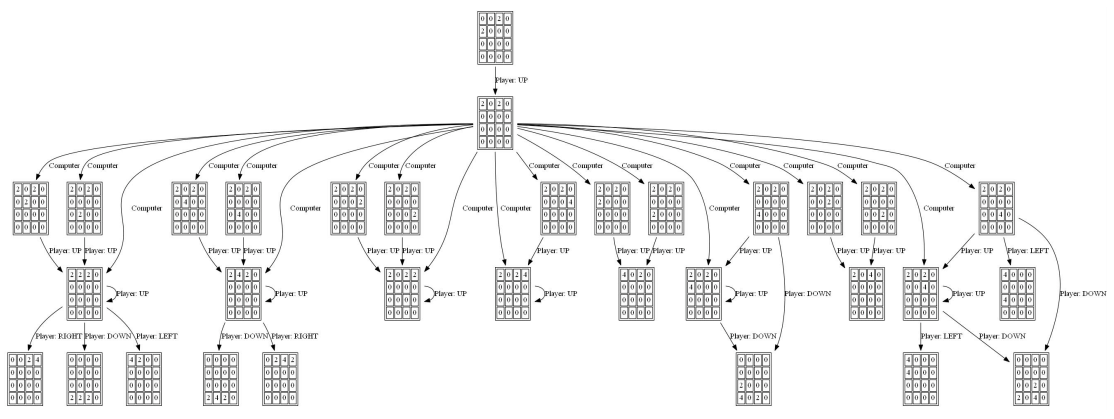

围棋的蒙特卡洛搜索树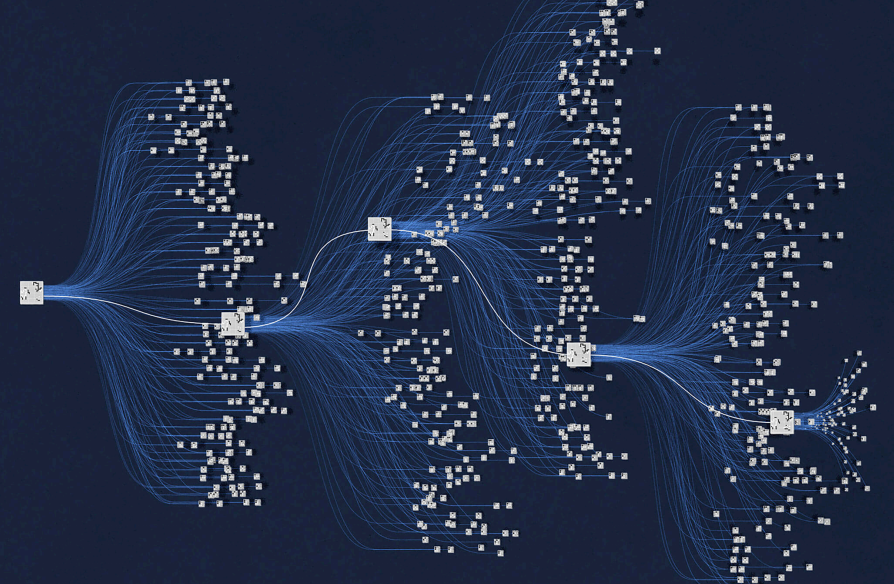

代码实战

问题一 N皇后（51）

问题描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

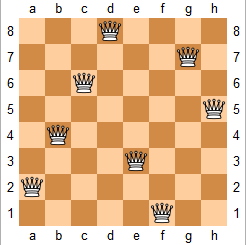
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

输入: 4
输出: [
[“ . Q . . “, // 解法 1
“ . . . Q “,
“ Q . . . “,
“ . . Q . “],
[“ . . Q . “, // 解法 2
“ Q . . . “,
“ . . . Q “,
“ . Q . . “]
]
解释: 4 皇后问题存在两个不同的解法。

解题思路分析

解法代码

Java代码

class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<LinkedHashSet<Integer>> res = new ArrayList<>();
        DFS(n, res, new LinkedHashSet(), new LinkedHashSet(), new LinkedHashSet());
        List<List<String>> result = new ArrayList<>();
        List<String> string = null;
        for (LinkedHashSet<Integer> rol : res) {
            string = new ArrayList<>();
            for (int q : rol) {
                String str = "";
                int i = 0;
                while(i < q) {
                    str += ".";
                    i++;
                }
                str += "Q";
                while(i < n-1) {
                    str += ".";
                    i++;
                }
                string.add(str);
            }
            result.add(string);
        }
        return result;
    }
    
    public void DFS(int n, List<LinkedHashSet<Integer>> res, LinkedHashSet<Integer> cols, LinkedHashSet<Integer> pie, LinkedHashSet<Integer> na) {
        int row = cols.size();
        if (row == n) {
            LinkedHashSet<Integer> answer = new LinkedHashSet<>(cols);
            res.add(answer);
            return;
        }
        for (int col=0; col < n; col++) {
            if (!cols.contains(col) && !pie.contains(row+col) && !na.contains(row-col)) {
                cols.add(col);
                pie.add(row+col);
                na.add(row-col);
                DFS(n, res, cols, pie, na);
                cols.remove(col);
                pie.remove(row+col);
                na.remove(row-col);
            }
        }
    }
}

Python代码

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        if n < 1: return []
        self.result = []
        self.cols = set(); self.pie = set(); self.na = set()
        self.DFS(n, 0, [])
        return [["."*i + "Q" + "."*(n-i-1) for i in sol] for sol in self.result]
    
    def DFS(self, n, row, cur_state):
        # recursion terminator
        if row >= n:
            self.result.append(cur_state)
            return
        
        for col in range(n):
            if col in self.cols or row+col in self.pie or row-col in self.na:
                # go die
                continue
            
            # update this flags
            self.cols.add(col)
            self.pie.add(row+col)
            self.na.add(row-col)
            
            self.DFS(n, row+1, cur_state+[col])
            
            self.cols.remove(col)
            self.pie.remove(row+col)
            self.na.remove(row-col)

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        if n < 1: return []
        self.result = []
        self.DFS(n, [], [], [])
        return [["."*i + "Q" + "."*(n-i-1) for i in sol] for sol in self.result]
    
    def DFS(self, n, cols, pie, na):
        # recursion terminator
        row = len(cols)
        if row == n:
            self.result.append(cols)
            return None
        
        for col in range(n):
            if col not in cols and row+col not in pie and row-col not in na:
                self.DFS(n, cols+[col], pie+[row+col], na+[row-col])

总结：Python 的第二段代码更加简洁，为第一段代码的改进。在第一段的基础上将 set 改为 list 直接传入函数！Java 的代码按照 Python 的思路来写一直无法通过，主要原因在于写入答案时，一定要将答案拷贝一份再存入最终结果数组 res 中。

问题二解数独（37）

问题描述

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

空白格用 '.' 表示。

一个数独。

答案被标成红色。

Note:

给定的数独序列只包含数字 1-9 和字符 ‘.’ 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。

解题思路分析

方法一

设置集合 set ：row[9], col[9], block[3][3]，用于判断空白格子填入数字的合法性。
利用 DFS 按照先行后列的顺序依次遍历空格，枚举 1-9 中的数字填入空格，并判断填入数字的合法性。

方法二

在 方法一 的基础上进行改进，先枚举行和列空格较少的位置，因为枚举的选项较少，可以起到加速的效果。
预处理数据，扫描整个表格，将空格能够填入的数字列举出来，并对每个空格能够填入数字的数量进行排序。按照由小到大的顺序进行 DFS 搜索。

方法三 使用高级数据结构

DancingLink，了解即可。

解法代码

Java代码

class Solution {
    public void solveSudoku(char[][] board) {
        if (board == null || board.length == 0) return;
        solve(board);
    }
    public boolean solve(char[][] board) {
        for (int i = 0; i < board.length; i++)
            for (int j = 0; j < board[i].length; j++) {
                if (board[i][j] == '.') {
                    for (char c = '1'; c <= '9'; c++) {
                        if (isValid(board, i, j, c)) {
                            board[i][j] = c;
                            if (solve(board))
                                return true;
                            else
                                board[i][j] = '.';
                        }
                    }
                    return false;
                }
            }
        return true;
    }
    private boolean isValid(char[][] board, int row, int col, char c) {
        for (int i=0; i < 9; i++) {
            if (board[i][col] != '.' && board[i][col] == c) return false;
            if (board[row][i] != '.' && board[row][i] == c) return false;
            if (board[3 * (row/3) + i/3][3 * (col/3) + i%3] != '.'
               && board[3 * (row/3) + i/3][3 * (col/3) + i%3] == c) return false;
        }
        return true;
    }
}

Python代码

class Solution:
    def solveSudoku(self, board: List[List[str]]) -> None:
        """
        Do not return anything, modify board in-place instead.
        """
        if board == [] or len(board) == 0: return;
        self.solve(board)

        
    def solve(self, board: List[List[str]]) -> bool:
        for i in range(len(board)):
            for j in range(len(board[i])):
                if board[i][j] == ".":
                    for c in range(1, 10):
                        c = str(c)
                        if self.isValid(board, i, j, c):
                            board[i][j] = c
                            if (self.solve(board)):
                                return True
                            else:
                                board[i][j] = "."
                    return False
        return True
    
    def isValid(self, board: List[List[str]], row: int, col: int, c: str) -> bool:
        for i in range(9):
            if board[i][col] !='.' and board[i][col] == c: return False
            if board[row][i] !='.' and board[row][i] == c: return False
            if board[3*(row//3)+i//3][3*(col//3)+i%3] !='.' and board[3*(row//3)+i//3][3*(col//3)+i%3] == c: return False
        return True

二分查找（Binary Search）

Sorte（单调递增或者递减）
Bounded（存在上下界）
Accessible by index（能够通过索引访问）

代码模板

二分查找示例图

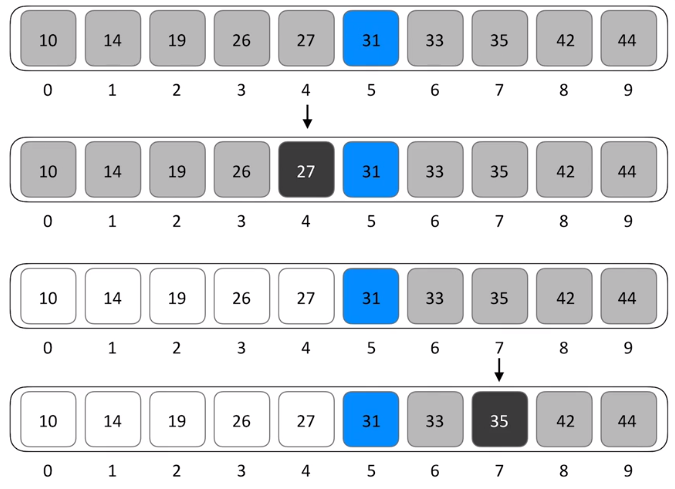
代码实战

问题一 x 的平方根（69）

问题描述

实现 int sqrt(int x) 函数。计算并返回 x 的平方根，其中 x 是非负整数。
由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2

示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842…,
由于返回类型是整数，小数部分将被舍去。

解题思路分析

方法一，二分法：
因为 $y = x^2$ 是单调递增函数，所以可以使用二分法。令左界 L = 0 ，右界 R = y，mid = (L+R)/2，若 mid*mid < y，搜索右侧[mid, R]；反之搜索左侧[L, mid] 。
方法二，牛顿迭代法：
令 $f(x) = x^2 - y$，$x_{n+1} = x_n - \frac {f(x_n)}{f^{‘}(x_n) } $ ，不停循环迭代即可以逼近真实值。

解法一：二分法

Java代码

class Solution {
    public int mySqrt(int x) {
        if (x == 0 || x == 1) return x;
        int l = 0, r = x, res=0;
        while (l <= r) {
            int mid = (l+r)/2;
            if (mid == x/mid) return mid;
            if (mid > x/mid)
                r = mid-1;
            else {
                l = mid+1;
                res = mid;
            }
        }
        return res;
    }
}

Python代码

class Solution:
    def mySqrt(self, x: int) -> int:
        if x == 1 or x == 0: return x
        l, r, res = 0, x, 0
        while l <= r:
            mid = (l + r)//2
            if mid**2 == x:
                return mid
            elif mid**2 < x:
                l = mid + 1
                res = mid
            else:
                r = mid - 1
        return res

解法二：牛顿迭代法

Java代码

class Solution {
    public int mySqrt(int x) {
        double r = x;
        while (Math.abs(r * r - x) > 0.5)
            r = (r + x / r) / 2;
        return (int)r;
    }
}

Python代码

class Solution:
    def mySqrt(self, x: int) -> int:
        r = x
        while abs(r**2 - x) > 0.5:
            r = (r + x/r) / 2
        return int(r)

字典树（trie）

Trie 树的数据结构
Trie 树的核心思想
Trie 树的基本性质

基本结构

Trie 树，即字典树，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串(但不仅限于字符串)，所以经常被搜索引擎系统用于文本词频统计。

它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。

核心思想

Trie 的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

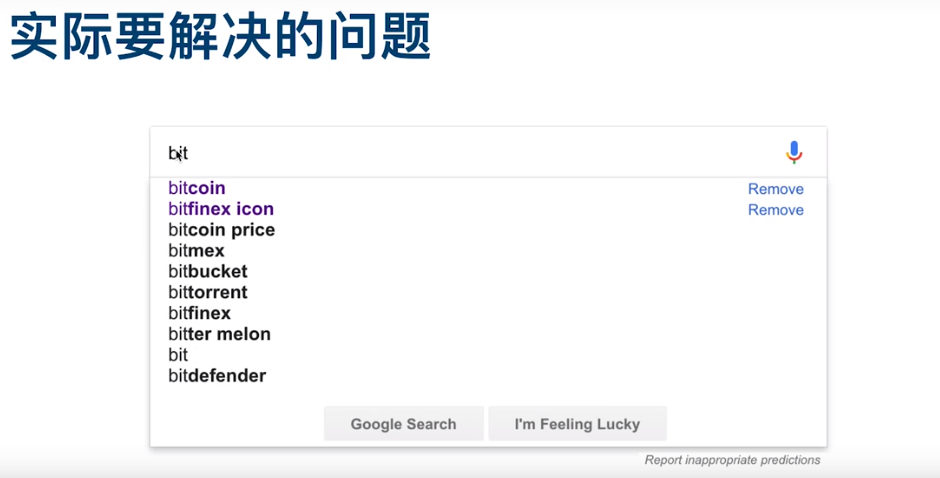
存储结构

不同变成语言的结构实现

Java

Python

基本性质

根节点不包含字符，除根节点外每一个节点都只包含一个字符，或者不包含字符。
从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
每个节点的所有子节点包含的字符都不相同。

代码实战

问题一实现 Trie (前缀树)（208）

问题描述

实现一个 Trie (前缀树)，包含 insert, search, 和 startsWith 这三个操作。

示例:

Trie trie = new Trie();

trie.insert(“apple”);
trie.search(“apple”); // 返回 true
trie.search(“app”); // 返回 false
trie.startsWith(“app”); // 返回 true
trie.insert(“app”);
trie.search(“app”); // 返回 true

说明:

你可以假设所有的输入都是由小写字母 a-z 构成的。
保证所有输入均为非空字符串。

解法代码

Java代码

class TrieNode {
    public char val;
    public boolean isWord;
    public TrieNode[] children = new TrieNode[26];
    public TrieNode() {}
    TrieNode(char c) {
        TrieNode node = new TrieNode();
        node.val = c;
    }
}

class Trie {
    private TrieNode root;
    /** Initialize your data structure here. */
    public Trie() {
        root = new TrieNode();
        root.val = ' ';
    }
    
    /** Inserts a word into the trie. */
    public void insert(String word) {
        TrieNode node = root;
        for(char c : word.toCharArray()) {
            if (node.children[c-'a'] == null)
                node.children[c-'a'] = new TrieNode(c);
            node = node.children[c-'a'];
        }
        node.isWord = true;
    }
    
    /** Returns if the word is in the trie. */
    public boolean search(String word) {
        TrieNode node = root;
        for(char c : word.toCharArray()) {
            if (node.children[c-'a'] == null) return false;
            node = node.children[c-'a'];
        }
        return node.isWord;
    }
    
    /** Returns if there is any word in the trie that starts with the given prefix. */
    public boolean startsWith(String prefix) {
        TrieNode node = root;
        for(char c : prefix.toCharArray()) {
            if (node.children[c-'a'] == null) return false;
            node = node.children[c-'a'];
        }
        return true;
    }
}

Python代码

class Trie:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.root = {}
        self.end_of_word = "#"

    def insert(self, word: str) -> None:
        """
        Inserts a word into the trie.
        """
        node = self.root
        for char in word:
            node = node.setdefault(char, {})
        node[self.end_of_word] = self.end_of_word

    def search(self, word: str) -> bool:
        """
        Returns if the word is in the trie.
        """
        node = self.root
        for char in word:
            if char not in node:
                return False
            node = node[char]
        return self.end_of_word in node

    def startsWith(self, prefix: str) -> bool:
        """
        Returns if there is any word in the trie that starts with the given prefix.
        """
        node = self.root
        for char in prefix:
            if char not in node:
                return False
            node = node[char]
        return True

问题二单词搜索 II（212）

问题描述

给定一个二维网格 board 和一个字典中的单词列表 words，找出所有同时在二维网格和字典中出现的单词。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

示例：

输入:
words = [“oath”,”pea”,”eat”,”rain”] and board =
[
[‘o’, ‘a’, ‘a’, ‘n’],
[‘e’, ‘t’, ‘a’, ‘e’],
[‘i’, ‘h’, ‘k’, ‘r’],
[‘i’, ‘f’, ‘l’, ‘v’]
]
输出: [“eat”,”oath”]

说明：
你可以假设所有输入都由小写字母 a-z 组成。

提示：

你需要优化回溯算法以通过更大数据量的测试。你能否早点停止回溯？
如果当前单词不存在于所有单词的前缀中，则可以立即停止回溯。什么样的数据结构可以有效地执行这样的操作？散列表是否可行？为什么？前缀树如何？如果你想学习如何实现一个基本的前缀树，请先查看这个问题：实现Trie（前缀树）。

解题思路分析

方法一，DFS
方法二，Trie

解法代码

Java代码

class Solution {
    Set<String> res = new HashSet<String>();
    
    public List<String> findWords(char[][] board, String[] words) {
        Trie trie = new Trie();
        for (String word: words)
            trie.insert(word);
        int n = board.length;
        int m = board[0].length;
        boolean[][] visited = new boolean[n][m];
        for (int i=0; i < n; i++)
            for (int j=0; j < m; j++) {
                dfs(board, visited, "", i, j, trie);
            }
        return new ArrayList<String>(res);
    }
    
    public void dfs(char[][] board, boolean[][] visited, String str, int i, int j, Trie trie) {
        if (i < 0 || i >= board.length || j < 0 || j >= board[0].length) return;
        if (visited[i][j]) return;
        
        str += board[i][j];
        if (!trie.startsWith(str)) return;
        
        if (trie.search(str)) {
            res.add(str);
        }
        visited[i][j] = true;
        dfs(board, visited, str, i-1, j, trie);
        dfs(board, visited, str, i+1, j, trie);
        dfs(board, visited, str, i, j-1, trie);
        dfs(board, visited, str, i, j+1, trie);
        visited[i][j] = false;
    }
}

Python代码

dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
END_OF_WORD = "#"

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        if not board or not board[0]: return []
        if not words: return []
        
        self.result = set()
        root = collections.defaultdict()
        for word in words:
            node = root
            for char in word:
                node = node.setdefault(char,collections.defaultdict())
            node[END_OF_WORD] = END_OF_WORD
            
        self.n, self.m = len(board), len(board[0])
        
        for i in range(self.n):
            for j in range(self.m):
                if board[i][j] in root:
                    self._dfs(board, i, j, "", root)
                    
        return list(self.result)
    
    def _dfs(self, board, i, j, cur_word, cur_dict):
        cur_word += board[i][j]
        cur_dict = cur_dict[board[i][j]]
        
        if END_OF_WORD in cur_dict:
            self.result.add(cur_word)
            
        tmp, board[i][j] = board[i][j], "@"
        for k in range(4):
            x, y = i + dx[k], j + dy[k]
            if 0 <= x < self.n and 0 <= y < self.m \
                and board[x][y] != "@" and board[x][y] in cur_dict:
                self._dfs(board, x, y, cur_word, cur_dict)
        board[i][j] = tmp

总结：Java 代码的解答过程思路比较清晰，但是光运行上述代码是不行的，还用到了上题中的 Trie 数据结构。Python 的代码比较简洁，对于数据访问的标记比较巧妙，不像 Java 开辟了一部分内存 visited 专门用来记录元素的访问情况。

递归 & 分治

Recursion 递归 — 循环

递归代码通用模板

分治 - Divde & Conquer

分治代码通用模板

代码实战

问题一 Pow(x, n)（50）

问题描述

解题思路分析

解法代码

问题二 求众数（169）

问题描述

解题思路分析

解法代码

贪⼼算法（Greedy Algorithms)

概念

适⽤ Greedy 的场景

代码实战

问题一 买卖股票的最佳时机 II（122）

问题描述

解题思路分析

解法代码

⼴度优先搜索(BFS) 与 深度优先搜索(DFS)

⼴度优先搜索(Breadth-First-Search)

在树（图/状态集）中寻找特定节点

BFS 如何工作

BFS 代码

深度优先搜索(Depth-First-Search)

DFS 如何工作

DFS 代码

代码实战

问题一 二叉树的层次遍历（102）

问题描述

解题思路分析

解法代码

问题二 二叉树的最大深度（104）

问题描述

解题思路分析

解法一：Recursion

解法二：BFS or DFS

问题三 二叉树的最小深度（111）

问题描述

解题思路分析

解法代码

问题四 括号生成（22）

问题描述

解题思路分析

解法代码

剪枝

剪枝图例

代码实战

问题一 N皇后（51）

问题描述

解题思路分析

解法代码

问题二 解数独（37）

问题描述

解题思路分析

解法代码

二分查找（Binary Search）

代码模板

二分查找示例图

代码实战

问题一 x 的平方根（69）

问题描述

解题思路分析

解法一：二分法

解法二：牛顿迭代法

字典树（trie）

基本结构

核心思想

不同变成语言的结构实现

基本性质

代码实战

问题一 实现 Trie (前缀树)（208）

问题描述

解法代码

问题二 单词搜索 II（212）

问题描述

解题思路分析

问题二求众数（169）

问题一买卖股票的最佳时机 II（122）

⼴度优先搜索(BFS) 与深度优先搜索(DFS)

问题一二叉树的层次遍历（102）

问题二二叉树的最大深度（104）

问题三二叉树的最小深度（111）

问题四括号生成（22）

问题二解数独（37）

问题一实现 Trie (前缀树)（208）

问题二单词搜索 II（212）