LSA概论
LSA(latent semantic analysis) 潜在语义分析,也被称为 LSI(latent semantic index),是 Scott Deerwester,Susan T.Dumais 等人在1990年提出来的一种新的索引和检索方法。该方法和传统向量空间模型 (vector space model) 一样使用向量来表示词 (terms) 和文档 (documents),并通过向量间的关系(如夹角)来判断词及文档间的关系;而不同的是,LSA 将词和文档映射到 潜在语义空间,从而去除了原始向量空间中的一些 “噪音”,提高了信息检索的精确度。
传统向量空间模型使用精确的词匹配,即精确匹配用户输入的词与向量空间中存在的词。由于一词多义 (polysemy) 和一义多词 (synonymy) 的存 在,使得该模型无法提供给用户语义层面的检索。比如用户搜索 “automobile”,即汽车,传统向量空间模型仅仅会返回包含 “automobile” 单词的页面,而实际上包含 “car” 单词的页面也可能是用户所需要的。
LSA 潜在语义分析的目的,就是要找出词 (terms) 在文档和查询中真正的含义,也就是潜在语义,从而解决上节所描述的问题。具体说来就是对一个大型的文档集合使用一个合理的维度建模,并将词和文档都表示到该空间,比如有2000个文档,包含7000个索引词,LSA 使用一个维度为100 的向量空间将文档和词表示到该空间,进而在该空间进行信息检索。而将文档表示到此空间的过程就是 SVD 奇异值分解和降维的过程。降维是 LSA分析中最重要的一步,通过降维,去除了文档中的 “噪音”,也就是无关信息(比如词的误用或不相关的词偶尔出现在一起),语义结构逐渐呈现。相比传统向量空间,潜在语义空间的维度更小,语义关系更明确。
LSA的步骤
- 分析文档集合,建立Term-Document矩阵;
- 对Term-Document矩阵进行奇异值分解;
- 对SVD分解后的矩阵进行降维,也就是奇异值分解一节所提到的低阶近似;
- 使用降维后的矩阵构建潜在语义空间,或重建Term-Document矩阵。
SVD奇异值分解
我们都知道,一个矩阵其实代表了一个线性变换(旋转,拉伸),可以将一个线性变换过程分解多个子过程,矩阵奇异值分解就是将矩阵分解成若干个秩一矩阵的和。
$$ A = \sigma _ { 1 } u _ { 1 } v _ { 1 } ^ { T } + \sigma _ { 2 } u _ { 2 } v _ { 2 } ^ { T } + \cdots + \sigma _ { n } u _ { n } v _ { n } ^ { T } $$
其中 $ \sigma_i $ 是奇异值,$ u_i v_i^T $ 是秩为 1 的矩阵,表示一个线性变换子过程。奇异值 $ \sigma_i $ 反映了该过程 $ u_i v_i^T $ 在该线性变换 $ A $ 中的重要程度。对上面式子进行整理,我们可以将奇异值分解过程写成如下:
$$ A = U \Sigma V ^ { T } $$
其中,$ U $ 是左奇异向量构成的矩阵,两两相互正交,$ \Sigma $ 是奇异值构成的对角矩阵,$ V^T $ 是右奇异向量构成的矩阵,两两相互正交。
定理:令 $ r $ 是 $ M×N $ 矩阵 $ A $ 的秩,那么 $ A $ 存在如下形式的 SVD :
$$ A = U \Sigma V ^ { T } $$
其中
(1)$ CC^T $ 的特征值 $ \lambda_1 $, $ \lambda_2 $, … , $ \lambda_r $ 等于 $ C^TC $的特征值;
(2)对于 $ 1 \le i \le r $,令 $ \sigma_i = \sqrt { \lambda_i } $,并且 $ \sqrt { \lambda_i } \ge \sqrt { \lambda_{i+1} } $。$ M×N $ 的矩阵 $ \Sigma $ 满足 $ \Sigma_{ii} = \sigma_i $,其中 $ 1 \le i \le r $,而 $ \Sigma $ 中其他元素均为 0。
对于奇异值分解的定理,这里我们不加以证明,有兴趣的同学参考 矩阵分析 相关知识。
分解后的矩阵形式如下:
$$ \begin{bmatrix}
\centerdot & \centerdot & \centerdot \\
\centerdot & \centerdot & \centerdot \\
\centerdot & \centerdot & \centerdot \\
\centerdot & \centerdot & \centerdot \\
\centerdot & \centerdot & \centerdot \end{bmatrix} =
\begin{bmatrix}
\centerdot & \centerdot & \centerdot & \centerdot & \centerdot \\
\centerdot & \centerdot & \centerdot & \centerdot & \centerdot \\
\centerdot & \centerdot & \centerdot & \centerdot & \centerdot \\
\centerdot & \centerdot & \centerdot & \centerdot & \centerdot \\
\centerdot & \centerdot & \centerdot & \centerdot & \centerdot \end{bmatrix} \times
\begin{bmatrix}
\centerdot & & \\
& \centerdot & \\
& & \centerdot \\ \\ \end{bmatrix} \times
\begin{bmatrix}
\centerdot & \centerdot & \centerdot \\
\centerdot & \centerdot & \centerdot \\
\centerdot & \centerdot & \centerdot \end{bmatrix} $$
奇异值分解具有如下数学性质:
- 一个 $ m \cdot n $ 的矩阵至多有 $ p=min(m,n) $ 个不同的奇异值;
- 矩阵的信息往往集中在较大的几个奇异值中。
LSA 正是利用了奇异值分解的这两个性质,实现将原始的单词-文档矩阵映射到语义空间。
词项-文档矩阵及SVD分解
在 LSA 中,我们不再将矩阵理解成变换,而是看作文本数据的集合。文本语料中所有的单词构成了矩阵的行,每一列表示一篇文档(词袋模型表示)。假设$ A $是一个 $ m \cdot n $ 的文本数据矩阵($ n \ll m $),表示该语料包含 $ m $ 个单词,$ n $ 篇文档。这 $ m $ 个单词中肯定存在同义词等,这样一篇文档用 $ m $ 维特征表示就显得冗余,不利于计算。利用矩阵奇异值分解:
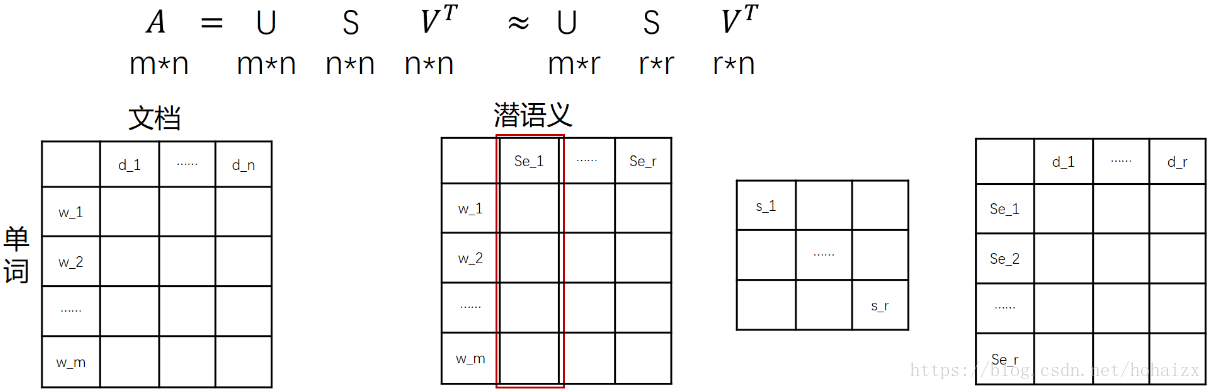
依据奇异值分解的性质1,矩阵 $ A $ 可以分解出 $ n $ 个特征值,然后依据性质2,我们选取其中较大的 $ r $ 个并排序,这样 $ U \Sigma V ^ { T } $ 就可以近似表示矩阵 $ A $。对于矩阵 $ U $,每一列代表一个潜语义,这个潜语义的意义由 $ m $ 个单词按不同权重组合而成。因为 $ U $ 中每一列相互独立,所以 $ r $ 个潜语义构成了一个语义空间。$ \Sigma $ 中每一个奇异值指示了该潜语义的重要度。$ V^T $中每一列仍然是一篇文档,但此时文档被映射到了语义空间。$ V^T $的大小远小于 $ A $,或者说 $ V^T $ 中列向量的维度远小于 $ A $ 中列向量的维度。
有了 $ V^T $,我们就相当于有了矩阵 $A$ 的另外一种表示,之后我们就可以使用 $V^T$ 代替 $A$ 进行之后的工作。
假如我们有如下词项-文档矩阵
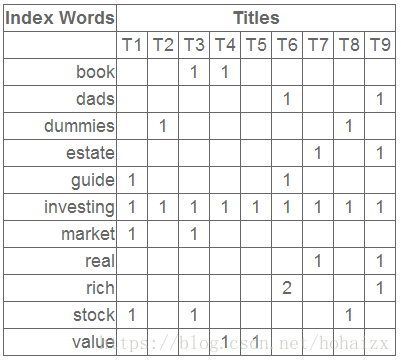
这个矩阵的一行表示一个单词在哪些 title 中出现了(一行就是之前说的一维特征),一列表示一个 title 中包含哪些词,对这个矩阵进行奇异值分解,并选取奇异值最大的三项,得到下面矩阵:
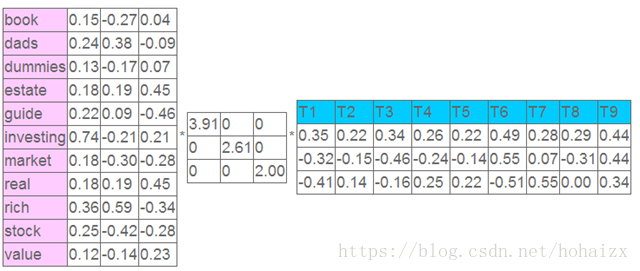
表示我们将文档映射到了一个 3 维语义空间中,其中第一维潜语义可以表示为:
$$ topoic1: book \cdot 0.15 + dads \cdot 0.24 + dummies \cdot 0.13 + \cdots + stock \cdot 0.25 + value \cdot 0.12 $$
同时单词 book 在该语义空间中的向量表示为 (0.15,−0.27,0.04)。此时 title1 在该语义空间中的向量表示是 (0.35,−0.32,−0.41)。然后我们反过头来看,我们可以将左奇异向量和右奇异向量都取后2维(之前是3维的矩阵),投影到一个平面上,可以得到:
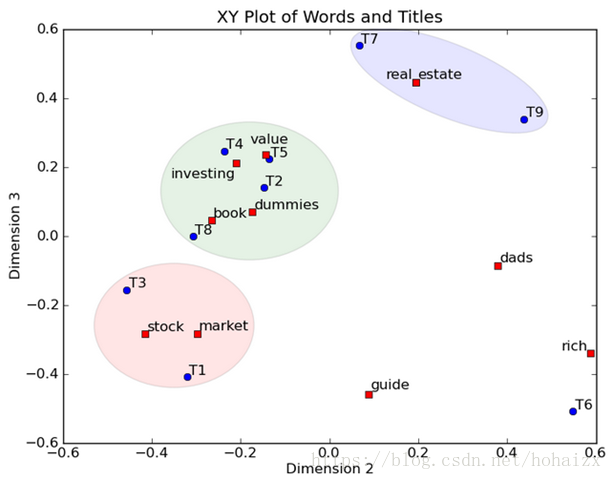
在图上,每一个红色的点,都表示一个词,每一个蓝色的点,都表示一个 title,这样我们可以对这些词和 title 进行聚类,比如 stock 和 market 可以放在一类,这也符合他们经常出现在一起的直觉,real 和 estate 可以放在一类,dads,guide 这种词就看起来有点孤立了,我们就不对他们进行合并了。对于 title,T1 和 T3 可以聚成一类,T2、T4、T5 和 T8 可以聚成一类,所以 T1 和 T3 比较相似,T2、T4、T5 和 T8 比较相似。按这样聚类出现的效果,可以提取文档集合中的近义词,这样当用户检索文档的时候,是用语义级别(近义词集合)去检索了,而不是之前的词的级别。这样一减少我们的检索、存储量,因为这样压缩的文档集合和主成分分析 PCA 的降维思想(低秩逼近原理,后文解释)是异曲同工的,二可以提高我们的用户体验,用户输入一个词,我们可以在这个词的近义词的集合中去找,这是传统的索引无法做到的。
低秩逼近
前面介绍了一个 SVD 分解的例子,下面我们来看看一个矩阵逼近问题,我们可以利用 SVD 对该问题求解,然后应用于其他领域。
给定 $ M×N $ 的矩阵 $ A $ 及正整数 $ k $,寻找一个秩不高于 $ k $ 的 $ M×N $ 的矩阵 $ A_k $,使得两个矩阵的差 $ X = A - A_k $ 的 F范数 最小,即下式最小:
$$ | x | _ { F } = \sqrt { \sum _ { i = 1 } ^ { M } \sum _ { j = 1 } ^ { N } X _ { i j } ^ { 2 } } $$
$ X $ 的 F范数 度量了 $ A_k $ 和 $ A $ 之间的差异程度。当 $ k $ 比 $ r $ 小得多时,我们称 $ A_k $ 为低秩逼近矩阵。
SVD 可以用来解决矩阵低秩逼近问题,为此,我们要进行如下3步骤:
- 给定 $ A $,构造 SVD 分解,因此 $ A = U \Sigma V ^ { T } $;
- 把 $ \Sigma $ 中对角线上 $ r - k $ 个最小奇异值置为0,从而得到 $ \Sigma_k $;
- 计算 $ A_k = U \Sigma_k V^T $ 作为 $ A $ 的逼近。
定理:
$$ \min _ { Z | rankk ( Z ) = k } | A - Z | _ { F } = \left| A - A _ { k } \right| _ { F } = \sqrt { \sum _ { i = k + 1 } ^ { r } \sigma _ { i } ^ { 2 } } $$
由于奇异值按照降序排列,$ \sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_r $,我们从上述定义可以知道 $ A_k $ 是 $ A $ 的秩为 $ k $ 的最佳逼近,其中误差的大小(采用 $ A - A_k $ 的 F范数 来度量)等于 $ \sqrt { \sum _ { i = k + 1 } ^ { r } \sigma _ { i } ^ { 2 } } $ 。所以 $ k $ 越大,误差越小,当 $ k = r $ 时,由于 $ \Sigma_r = \Sigma $,所以误差为0。给定 $ r \le M,N $ 的话,有 $ \sigma_{r+1} = 0 $,因此 $ A_k = A $ 。
为了深入理解为什么从 $ \Sigma $ 去掉最小的 $ r -k $ 个奇异值的过程能够产生低误差的k-秩逼近,我们考察下 $ A_k $ 的形式:
$$ A _ { k } = U \Sigma _ { k } V ^ { T } $$
$$ = U \left[ \begin{array} { c c c c c } { \sigma _ { 1 } } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { \ldots } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { \sigma _ { k } } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { \ldots } \end{array} \right] V ^ { T } $$
$$ = \sum _ { i = 1 } ^ { k } \sigma _ { i } \vec { u _ { i } } \vec { v _ { i } } ^ { T } $$
其中,$ \vec { u_i } $ 和 $ \vec { v_i } $ 分别是 $ U $ 和 $ V $ 的第 $ i $ 列。因此,$ \vec { u_i } \vec { v_i } ^ T $ 是一个 1-秩矩阵,于是我们将 $ A_k $ 表示成 $ k $ 个 1-秩矩阵 的加权和,每个矩阵的权重是一个奇异值。由于 $ \sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_k $,所以当 $ i $ 增加时,1-秩矩阵 $ \vec { u_i } \vec { v_i } ^ T $ 的权重也随之减小。
SVD分解的其他应用
从上面的低秩逼近理论我们不难发现,只要现实生活中能够建模为矩阵 $ A_{M \times N} $ 的问题,都可以通过 LSA 的方法将其原始数据映射到低维空间中。
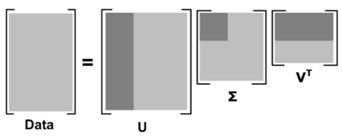
比如推荐系统,矩阵 A_{M \times N} 如果 $ M $ 代表商品个数,$ N $ 代表用户个数,则 $ U $ 矩阵每行代表商品属性,现在通过降维 $ U $ 矩阵(取阴影部分)后,每个商品的属性可以用更低的维度表示(假设k维)。这样当新来一个用户的商品推荐向量 $ X $,则可以根据公式 $ XU1inv(S1) $ 得到一个 $ k $维的向量,然后在 $ V^T $ 中寻找最相似的的那个用户(相似度计算可用余弦公式),根据这个用户的评分来推荐(主要是推荐新用户未打分的那些商品)。
SVD 在其他方面的应用除了隐形语义分析、隐形语义索引,还有信息检索、推荐引擎、图像压缩等。
相关文章
- http://www.ams.org/publicoutreach/feature-column/fcarc-svd:讲解SVD非常好的一篇文章,对于理解SVD非常有帮助,本文中SVD的几何意义就是参考这篇
- https://www.jianshu.com/p/9613b26c8b03:简书上有个人把上面的文章翻译成了中文,看不懂英文的小伙伴参见此链接
- http://http://blog.csdn.net/xiahouzuoxin/article/details/41118351 :讲解SVD与特征值分解区别的一篇文章
