隐马尔科夫模型定义

隐马尔可夫模型 (hidden Markov model,HMM) 是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列，称为状态序列 (state sequence)；每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列 (observation sequence)。序列的每一个位置又可以看作是一个时刻。

隐马尔科夫模型的数学表达

设 $ Q $ 是所有可能的状态的集合，$ V $ 是所有可能的观测的集合。

$$ Q=\lbrace q_1,q_2,\cdots,q_N \rbrace, V=\lbrace v_1,v_2,\cdots,v_M\rbrace $$

其中，$ N $ 是可能的状态数，$ M $ 是可能的观测数。状态 $ q $ 是不可见的，观测 $ v $ 是可见的。

$I$ 是长度为 $T$ 的状态序列，$O$ 是对应的观测序列。

$$ I=\lbrace i_1,i_2,\cdots,i_T\rbrace,O=\lbrace o_1,o_2,\cdots,o_T\rbrace $$

$A$ 为状态转移概率矩阵：

$$ A = \begin{bmatrix} a_{ij} \end{bmatrix}_{N \times N} $$

其中:

$ a_{ij} = P(i_{t+1}=q_j|i_t=q_i),i=1,2,\cdots,N;j=1,2,\cdots,N $ 是在时刻 $t$ 处于状态 $q_i$ 的条件下在时刻 $t$+1 转移到状态 $q_j$ 的概率。

B是观测概率矩阵:

$$ B = \begin{bmatrix} b_j(k) \end{bmatrix}_{N \times M} $$

其中，

$ b_j(k)=P(o_t=v_k|i_t=q_j),k=1,2,\cdots,M;j=1,2,\cdots,N $ 是在时刻t处于状态 $q_j$ 的条件下生成观测 $v_k$ 的概率（也就是所谓的“发射概率”）,在其它资料中，常见到的生成概率与发射概率其实是一个概念。

$\pi$ 是初始状态概率向量：$\pi=(\pi_i)$

其中，$ \pi_i=P(i_1=q_i),i=1,2,\cdots,N $ 是 $t$=1时刻处于状态 $q_i$ 的概率。

隐马尔可夫模型由初始状态概率向量 $π$、状态转移概率矩阵 $A$ 和观测概率矩阵 $B$ 决定。$π$ 和 $A$ 决定状态序列，$B$ 决定观测序列。因此，隐马尔可夫模型可以用三元符号表示，即

$$ \lambda=(A,B,\pi) $$

$A,B,\pi$ 称为隐马尔可夫模型的三要素。如果加上一个具体的状态集合 $Q$ 和观测序列 $V$，构成了 HMM 的五元组，这也是隐马尔科夫模型的所有组成部分。

HMM在NLP中的应用

HMM是可用于标注问题的统计学习模型，描述由隐藏的马尔可夫链随机生成观测序列的过程

1、应用到词性标注中，v 代表词语，是可以观察到的。q 代表我们要预测的词性（一个词可能对应多个词性）是隐含状态。
2、应用到分词中，v 代表词语，是可以观察的。q 代表我们的标签（B,E这些标签，代表一个词语的开始，或者中间等等）

3、应用到命名实体识别中，v 代表词语，是可以观察的。q 代表我们的标签（标签代表着地点词，时间词这些）

HMM实例解释

假设我手里有三个不同的骰子。第一个骰子是我们平常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6。第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4。第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。

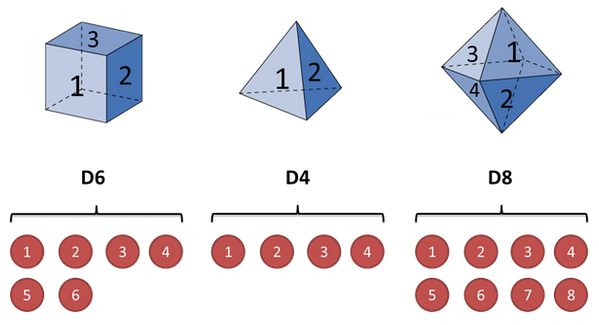
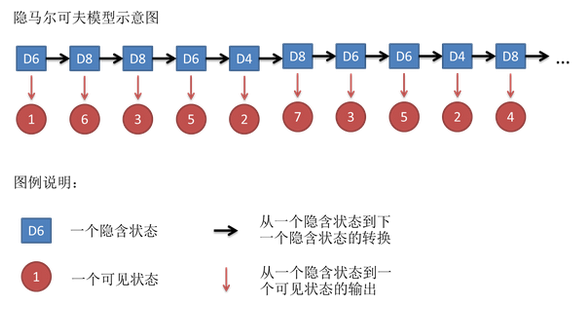
假设我们开始掷骰子，我们先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。然后我们掷骰子，得到一个数字，1，2，3，4，5，6，7，8中的一个。不停的重复上述过程，我们会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。例如我们可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4

这串数字叫做可见状态链（观测随机序列）。但是在隐马尔可夫模型中，我们不仅仅有这么一串可见状态链，还有一串隐含状态链。在这个例子里，这串隐含状态链就是你用的骰子的序列。比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8

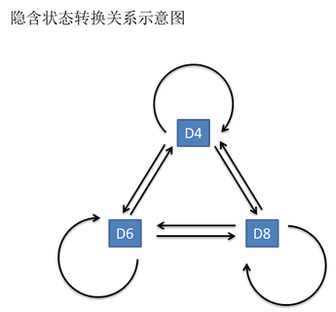
一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率（transition probability）。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

同样的，尽管可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率（emission probability）。就我们的例子来说，六面骰（D6）产生1的输出概率是1/6。产生2，3，4，5，6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。

其实对于HMM来说，如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率，做模拟是相当容易的。但是应用HMM模型时候呢，往往是缺失了一部分信息的，有时候你知道骰子有几种，每种骰子是什么，但是不知道掷出来的骰子序列；有时候你只是看到了很多次掷骰子的结果，剩下的什么都不知道。如果应用算法去估计这些缺失的信息，就成了一个很重要的问题。这些算法我会在下面详细讲。

隐马尔可夫链的三个基本问题

1、概率计算问题：给定模型 $\lambda=(A,B,\pi)$ 和观测序列 $O=(o_1,o_2,\cdots,o_T)$，计算在模型 $\lambda$ 下观测序列 $O$ 出现的概率 $P=(O|\lambda)$ 。
2、学习问题：已知观测序列 $O=(o_1,o_2,\cdots,o_T)$，估计模型 $\lambda=(A,B,\pi)$ 参数，使得在该模型下观测序列概率 $P=(O|\lambda)$ 最大。即用极大似然估计的方法估计参数。
3、预测问题：也称为解码（decoding）问题。已知模型 $\lambda=(A,B,\pi)$ 和观测序列 $O=(o_1,o_2,\cdots,o_T)$，求对给定观测序列条件概率 $P=(O|\lambda)$ 最大的状态序列 $I=\lbrace i_1,i_2,\cdots,i_T\rbrace$ 。即给定观测序列，求最有可能的对应的状态序列。

在介绍这三种常用算法之前我们先来了解一个常见的问题：知道骰子有几种，每种骰子是什么，每次掷的都是什么骰子，根据掷骰子掷出的结果，求产生这个结果的概率。

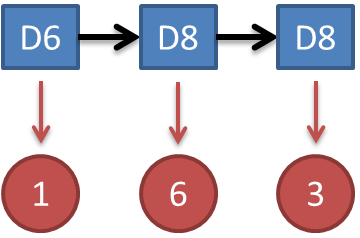
解法无非就是概率相乘：

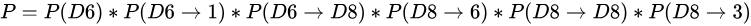
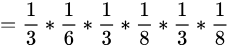
概率计算问题

前向算法

前向概率：给定隐马尔可夫模型 $\lambda$，定义到时刻 $t$ 部分观测序列为 $o_1,o_2,\cdots,o_t$ 且状态为 $q_i$ 的概率为前向概率，记作

$$ \alpha_t(i)=P(o_1,o_2,\cdots,o_t,i_t=q_i|\lambda) $$

可以递推地求得前向概率 $\alpha_t(i)$ 及观测序列概率 $P(O|\lambda)$ .

输入：隐马尔可夫模型 $\lambda$ ,观测序列 $O$ ；

输出：观测序列概率 $P(O|\lambda)$ .

1.初值

$$ \alpha_1(i)=\pi_ib_i(o_1),i=1,2,\cdots,N $$

2.递推 对 $t=1,2,\cdots,T-1,$

$$ \alpha_{t+1}(i)=\begin{bmatrix} \sum_{j=1}^N\alpha_t(j)a_{ji} \end{bmatrix} b_i(o_{t+1}) , i=1,2,\cdots,N $$

公式的意思就是当前观测结点的概率，其实是上一个观测结点的概率乘以转移概率（描述的是如何从上一个结点到当前结点的，有 $N$ 种走法可以到当前结点，求他们的概率和）最后再乘以当前观测对应发射矩阵内的值。

3.终止

$$ P(O|\lambda)=\sum_{i=1}^N\alpha_T(i) $$

意思就是将最终结点的（不同走法）的概率求和，就是产生目前观测的可能情况。

前向算法主要考虑前一个状态结点的概率（递推的内容），到达当前结点的走法（转移矩阵），当前观测和状态结点之间的关系（发射矩阵），将得到观测的各种可能走法综合起来（求和），就是一步一步从初值走到终点。

观察递推项，有木有觉得前向算法和维特比算法的递推项很相似，涉及到的都是前一个状态结点的概率、到达当前结点的“走法”（转移矩阵）、当前观测和当前状态的关系（发射矩阵）。不同的是，前向算法是“综合”各种可能情况，维特比算法是“挑选最优，动态规划”的思维，这个不同也体现在公式中，前者是 $\sum$，后者是 $max$ 。

后向算法

后向概率：给定隐马尔可夫模型 $\lambda$，定义在时刻 $t$ 状态为 $q_i$ 的条件下，从 $t$+1 到 $T$ 的部分观测序列为 $o_{t+1},o_{t+2},\cdots,o_T$ 的概率为后向概率，记作

$$ \beta_t(i)=P(o_{t+1},o_{t+2},\cdots,o_T|i_t=q_i,\lambda) $$

可以递推地求得前向概率 $\beta_t(i)$ 及观测序列概率 $P(O|\lambda)$

输入：隐马尔可夫模型 $\lambda$ ,观测序列 $O$；
输出：观测序列概率 $P(O|\lambda)$ .

1.初值

$$ \beta_T(i)=1,i=1,2,\cdots,N $$

2.递推 对 $t=T-1,T-2,\cdots,1,$

$$ \beta_t(i)=\sum_{j=1}^Na_{ij}b_j(o_{t+1})\beta_{t+1} (j),i=1,2,\cdots,N $$

公式的意思就是，当前的状态的概率跟后一个状态的概率和观测有关，同时要考虑多种（$N$种）当前状态向后一个状态的转移。

3.终止

$$ P(O|\lambda)=\sum_{i=1}^N\pi_ib_i(o_1) \beta_1(i) $$

由于初始观测已经确定，所以初始状态在哪个盒子里是由 $\pi$ 和 $B$ 共同决定的，考虑这个因素进去，再“综合”（求和）可以得到观测序列的各种情况，得到最终结果。

后向算法主要考虑当前状态结点的概率（递推的内容），这个概率与当前结点到后一个结点的“走法”（转移矩阵），后一个观测和状态结点之间的关系（发射矩阵），一步一步向前推理，将得到观测的各种可能走法综合起来（求和），是一个逆向思考的过程。我认为：

前向算法是 —— 现在这样，要得到 result，往后能怎么“走”？（求果）

后向算法是 —— 现在这样的 result，是当初怎么“走”造成的？（追因）

谁动了我的骰子？

知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道掷出这个结果的概率。

看似这个问题意义不大，因为你掷出来的结果很多时候都对应了一个比较大的概率。问这个问题的目的呢，其实是检测观察到的结果和已知的模型是否吻合。如果很多次结果都对应了比较小的概率，那么就说明我们已知的模型很有可能是错的，有人偷偷把我们的骰子給换了。

比如说你怀疑自己的六面骰被赌场动过手脚了，有可能被换成另一种六面骰，这种六面骰掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。你怎么办么？答案很简单，算一算正常的三个骰子掷出一段序列的概率，再算一算不正常的六面骰和另外两个正常骰子掷出这段序列的概率。如果前者比后者小，你就要小心了。

比如说掷骰子的结果是：

要算用正常的三个骰子掷出这个结果的概率，其实就是将所有可能情况的概率进行加和计算。同样，简单而暴力的方法就是把穷举所有的骰子序列，还是计算每个骰子序列对应的概率，但是这回，我们不挑最大值了，而是把所有算出来的概率相加，得到的总概率就是我们要求的结果。这个方法依然不能应用于太长的骰子序列（马尔可夫链）。

我们会应用一个和前一个问题类似的解法，只不过前一个问题关心的是概率最大值，这个问题关心的是概率之和。解决这个问题的算法叫做前向算法 (forward algorithm)。

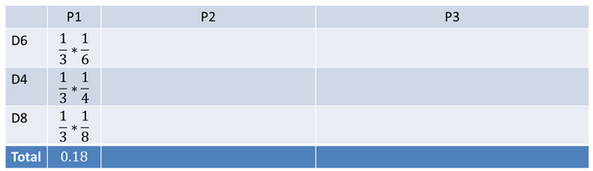
首先，如果我们只掷一次骰子：

看到结果为1.产生这个结果的总概率可以按照如下计算，总概率为0.18：

把这个情况拓展，我们掷两次骰子：

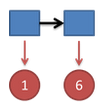
看到结果为1，6.产生这个结果的总概率可以按照如下计算，总概率为0.05：

继续拓展，我们掷三次骰子：

看到结果为1，6，3.产生这个结果的总概率可以按照如下计算，总概率为0.03：

同样的，我们一步一步的算，有多长算多长，再长的马尔可夫链总能算出来的。用同样的方法，也可以算出不正常的六面骰和另外两个正常骰子掷出这段序列的概率，然后我们比较一下这两个概率大小，就能知道你的骰子是不是被人换了。

学习问题

隐马尔可夫模型的学习，根据训练数据是包括观测序列和对应的状态序列还是只有观测序列，可以分别由监督学习与非监督学习实现。本节首先介绍监督学习算法，而后介绍非监督学习算法 Baum-Welch 算法（也就是EM算法）。

监督学习

假设已给训练数据包含 $S$ 个长度相同的观测序列和对应的状态序列 $\lbrace(O_1,I_1),(O_2,I_2),\cdots,(O_S,I_S)\rbrace$，那么可以利用极大似然估计法来估计隐马尔可夫模型的参数。具体方法如下：
1、转移概率 $a_{ij}$ 的估计
设样本中时刻 $t$ 处于状态 $i$ ，时刻 $t$+1 转移到状态 $j$ 的频数为 $A_{ij}$，那么状态转移概率 $a_{ij}$ 的估计是

$$ \hat {a}{ij} = \frac {A{ij}} {\sum_{j=1}^N A_{ij}},i=1,2,\cdots,N;j=1,2,\cdots,N $$

2、观测概率 $b_j(k)$ 的估计
设样本中状态为 $j$ 并观测为 $k$ 的频数是 $B_{jk}$，那么状态为 $j$ 观测为 $k$ 的概率 $b_j(k)$ 的估计是

$$ \hat{b}j(k) = \frac {B{jk}}{\sum_{k=1}^M B_{jk}},j=1,2,\cdots,N;k=1,2,\cdots,M $$

3、初始状态概率 $\pi_i$ 的估计 $\hat{\pi_i}$ 为 $S$ 个样本中初始状态为 $q_i$ 的频率

非监督学习（Baum-Welch算法）

Baum-Welch 算法的本质即 EM 算法，是用于含有隐向量的模型中，进行参数学习的迭代算法。回顾 EM 算法的核心，是按照 $\Theta(g+1)$ 和 $\Theta(g)$ 之间的等式关系：

假设给定训练数据只包含 $S$ 个长度为 $T$ 的观测序列 $\lbrace O_1,O_2,\cdots,O_S\rbrace$ 而没有对应的状态序列，目标是学习隐马尔可夫模型 $\lambda=(A,B,\pi)$ 的参数。我们将观测序列数据看作观测数据 $O$，状态序列数据看作不可观测的隐数据 $I$，那么隐马尔可夫模型事实上是一个含有隐变量的概率模型

$$ P(O|\lambda)=\sum_IP(O|I,\lambda)P(I|\lambda) $$

它的参数学习可以由EM 算法实现。

1、确定完全数据的对数似然函数
所有观测数据写成 $O=(o_1,o_2,\cdots,o_T)$，所有隐数据写成 $I=(i_1,i_2,\cdots,i_T)$，完全数据是 $(O,I)=(o_1,o_2,…,o_T,i_1,i_2,…,i_T)$ 。完全数据的对数似然函数是 $logP(O,I|\lambda)$ 。

2、EM 算法的 E 步：求 $Q$ 函数 $Q(\lambda,\bar\lambda)$，$Q$ 函数的定义为

$$ Q(\lambda,\bar\lambda) = E_I[logP(O,I|\lambda)|O,\bar{\lambda}] $$

转化为：

$$ Q(\lambda,\bar\lambda)=\sum_IlogP(O,I|\lambda)P(O,I|\bar{\lambda}) $$

其中， $\bar\lambda$ 是隐马尔可夫模型参数的当前估计值， $\lambda$ 是要极大化的隐马尔可夫模型参数。

$$ P(O,I|\lambda)=\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2) \cdots a_{i_{T-1}i_T}(o_T) $$

于是函数 $Q(\lambda,\bar\lambda)$ 可以写成：

$$ Q(\lambda,\bar\lambda)=\sum_Ilog\pi_{i_1}P(O,I|\bar{\lambda})+\sum_I(\sum_{t=1}^{T-1}loga_{i_ti_{t+1}})P(O,I|\bar\lambda)+\sum_I(\sum_{t=1}^Tlogb_{i_t}(o_t))P(O,I|\bar\lambda) $$

式中求和都是对所有训练数据的序列总长度T进行的。

3、EM 算法的 M 步：极大化 $Q$ 函数 $Q(\lambda,\bar\lambda)$ 求模型参数 $A,B,\pi$ 由于要极大化的参数在式中单独地出现在3个项中，所以只需对各项分别极大化。最后求得结果为：

$$ \pi_i=\frac{P(O,i_1=i|\bar{\lambda})}{P(O|\bar{\lambda})} $$

$$ a_{ij}=\frac{\sum_{t=1}^{T-1}P(O,i_t=i,i_{t+1}=j|\bar\lambda)}{\sum_{t=1}^{T-1}P(O,i_t=i,|\bar\lambda)} $$

$$ b_j(k)=\frac{\sum_{t=1}^{T}P(O,i_t=j|\bar\lambda)I(o_t=v_k)}{\sum_{t=1}^{T}P(O,i_t=j,|\bar\lambda)} $$

预测问题

维特比算法实际是用动态规划解隐马尔可夫模型预测问题，即用动态规划 (dynamic programming) 求概率最大路径（最优路径）。这时一条路径对应着一个状态序列。

我们先来看一下 HMM 的应用场景，这样可能会更有学习的动力! HMM 主要应用于词性标注，语音识别，句子切分，字素音位转换，局部句法剖析，语块分析，命名实体识别，信息抽取，异常行为检测等

词性标注问题

首先介绍一下什么是词性标注问题，比如我们有一句已经分词好的句子。

dog chase mouse

那么我们就可以进行词性标注为：

其中nn为名词，vv为动词。通过上面例子，我们就很容易看出词性标注的任务。那么我们来了一句话之后，比如我们的词性字典中有nn,vv,prp(代词)，我们怎么能够找到dog chase mouse 所对应的词性标注呢，如果每一个单词有nn，vv，prp三种可能，那么将会有 3*3*3=27 种可能，我们如何去挑选呢？

如下图：

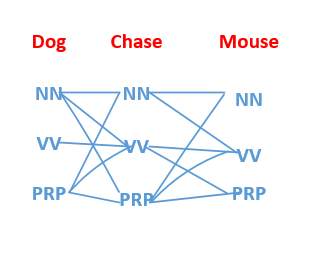
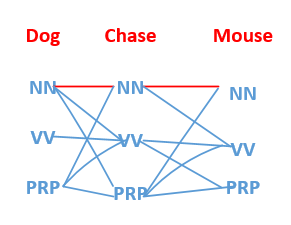
我们总共有27条路径，那么如何得到我们Dog chase mouse的最优路径呢？

我们至少可以遍历每一条路径，求出各自的概率值，然后挑选最大的即可，比如我们求第一条路径的时候，可以这么表示：

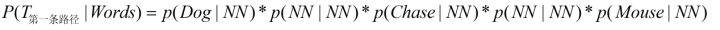
所求的路径对应如下图红色线条所示：

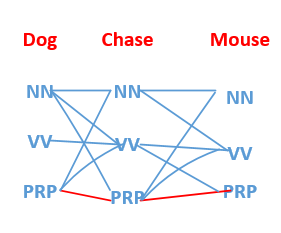
求第27条路径的时候，我们可以这么表示：

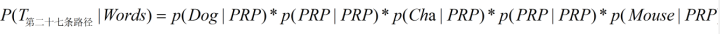
所求的路径对应如下图红色线条所示：

那么我们从上面可以知道，要求一个句子的最优词性标注，我们至少可以遍历所有的路径，然后挑选概率值最大的那条路径即可！！！

但是，给定模型，求给定长度为T的观测序列(这里指的就是Dog Chase Mouse)的概率，直接计算法的思路是枚举所有的长度T（例子中是三个，Dog，Chase，Mouse总共三个单词）的状态序列，计算该状态序列与观测序列的联合概率（隐状态发射到观测），对所有的枚举项求和即可。

在状态种类为N(例子中就是三个，NN，VV,PRP)的情况下，一共有$N^T$种排列组合，每种组合计算联合概率的计算量为T，总的复杂度为$O(TN^T)$，这并不可取。

于是维特比算法隆重登场了！！

维特比算法

首先导入两个变量 $\delta$ 和 $\Psi$。定义在时刻 $t$ 状态为 $i$ 的所有单个路径 $(i_1,i_2,\cdots,i_t)$ 中概率最大值为

$$ \delta_t(i) = \max_{i_1,i_2,\cdots,i_{t-1}}P(i_t=i,i_{t-1},\cdots,i_1,o_t,\cdots,o_1|\lambda),i=1,2,\cdots,N $$

由定义可得变量$\delta$的递推公式：

$$ \delta_{t+1}(i) = \max_{i_1,i_2,\cdots,i_t}P(i_{t+1}=i,i_t,\cdots,i_1,o_{t+1},\cdots,o_1|\lambda) $$
$$ = \max_{1 \le j \le N}[\delta_t(j) a_{ji}] b_i(o_{t+1}),i=1,2,\cdots,N;t=1,2,\cdots,T-1$$

定义在时刻 $t$ 状态为 $i$ 的所有单个路径$(i_1,i_2,\cdots,i_{t-1},i)$ 中概率最大的路径的第 $t$-1 个结点为

$$ \Psi_t(i) = arg\max_{1 \le j\le N}[\delta_{t-1}(j)a_{ji}], i=1,2,…,N $$

下面介绍维特比算法:

输入：模型 $\lambda=(A,B,\pi)$ 和观测 $O=(o_1,o_2,\cdots,o_T)$;

输出：最优路径 $ I=(i_1^\ast,i_2^\ast,\cdots,i_T^\ast) $

1、初始化

$$ \delta_1(i)=\pi_ib_i(o_1),i=1,2,\cdots,N $$

$$ \Psi_1(i)=0,i=1,2,\cdots,N $$

2、递推，对 $ t = 2,3,\cdots,T $

$$ \delta_t(i) = \max_{1\le j\le N}[\delta_{t-1}(j)a_{ji}]b_i(o_t),i=1,2,\cdots,N $$

$$ \Psi_t(i)=arg \max_{1\le j\le N}[\delta_{t-1}(j)a_{ji}],i=1,2,\cdots,N $$

3、终止

$$ P^\ast = \max_{1 \le i \le N}\delta_T(i) $$

$$ i_T^\ast = arg \max_{1 \le i \le N}[\delta_T(i)] $$

4、最优路径回溯，对 $t=T-1,T-2,\cdots,1$

$$ i_t^\ast = \Psi_{t+1}(i_{t+1}^\ast) $$

求得最优路径 $ I^\ast=(i_1^\ast,i_2^\ast,\cdots,i_T^\ast) $

看见不可见的，破解骰子序列

首先，如果我们只掷一次骰子：

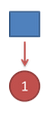
看到结果为1.对应的最大概率骰子序列就是D4，因为D4产生1的概率是1/4，高于1/6和1/8.

把这个情况拓展，我们掷两次骰子：

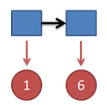
结果为1，6.这时问题变得复杂起来，我们要计算三个值，分别是第二个骰子是D6，D4，D8的最大概率。显然，要取到最大概率，第一个骰子必须为D4。这时，第二个骰子取到D6的最大概率是

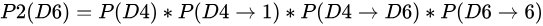
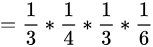
同样的，我们可以计算第二个骰子是D4或D8时的最大概率。我们发现，第二个骰子取到D6的概率最大。而使这个概率最大时，第一个骰子为D4。所以最大概率骰子序列就是D4 D6。

继续拓展，我们掷三次骰子：

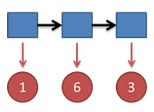
同样，我们计算第三个骰子分别是D6，D4，D8的最大概率。我们再次发现，要取到最大概率，第二个骰子必须为D6。这时，第三个骰子取到D4的最大概率是

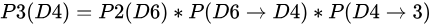
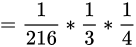
同上，我们可以计算第三个骰子是D6或D8时的最大概率。我们发现，第三个骰子取到D4的概率最大。而使这个概率最大时，第二个骰子为D6，第一个骰子为D4。所以最大概率骰子序列就是D4 D6 D4。

写到这里，大家应该看出点规律了。既然掷骰子一二三次可以算，掷多少次都可以以此类推。我们发现，我们要求最大概率骰子序列时要做这么几件事情。首先，不管序列多长，要从序列长度为1算起，算序列长度为1时取到每个骰子的最大概率。然后，逐渐增加长度，每增加一次长度，重新算一遍在这个长度下最后一个位置取到每个骰子的最大概率。因为上一个长度下的取到每个骰子的最大概率都算过了，重新计算的话其实不难。当我们算到最后一位时，就知道最后一位是哪个骰子的概率最大了。然后，我们要把对应这个最大概率的序列从后往前推出来。